3.5 Graphing Techiques: Transformations, 5.1 Exponential Functions, 6.3 Exponential Functions, Graphing Exponential Functions

Graphing an Exponential Equation by Transformations

Example: For the function below.  Graph using transformations.  Find the y-intercept.  State the horizontal asymptote and the domain and range.

f(x)=-2^{x+2}+2

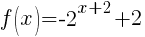
First we must examine the base function 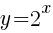y=2^x

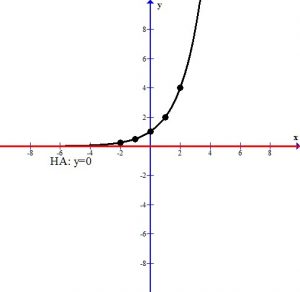
Graph using plotting points.  We can use the standard set of x-values to find ordered pairs.

xy
-22^(-2)=1/4
-12^(-1)=1/2
02^0=1
12^1=2
22^2=4

The graph below shows the points plotted and the line that connects them.  This graph has a horizontal asymptote at y=0.  The domain is 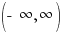(- infty, infty)  and the range is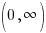 (0, infty)

 

Analyze the transformations.

f(x)=-2^{x+2}+2

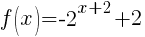
The +2 in the exponent shifts the graph left 2 units.

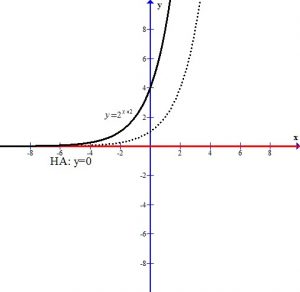
The – in the front of the base reflects the graph over the x-axis.

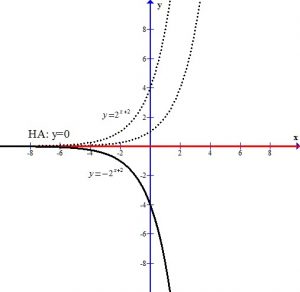
The +2 next to the base shifts the graph and the horizontal asymptote up two units.

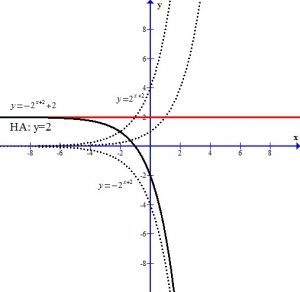
You can see the graph after the transformations.

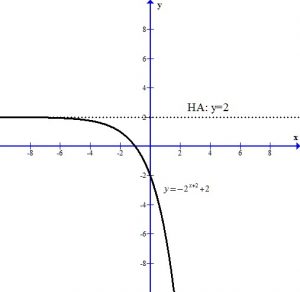
The horizontal asymptote is y=2.  The domain is 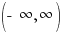(- infty, infty)  and the range is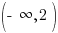 (- infty, 2)

To find the y-intercept we let x=0.

f(0)=-2^{0+2}+2

f(0)=-(2^{2})+2

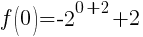
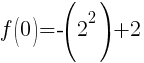
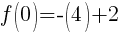
f(0)=-(4)+2

f(0)=-4+2

f(0)=-2

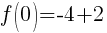
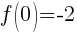
Thus the y-intercept is (0,-2)

Here is a youtube video with examples.