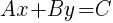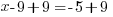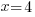Category Archives: Equations
Finding the Equation of a Line: Given a parallel line in standard form and a point on the line
Logarithmic Equations: Convert to Exponential
Solve an exponential equation: Take the log of both sides
Example:
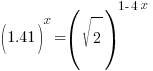
Solution:
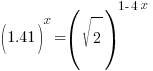 |
|
| Since the bases cannot be easily written the same use the method of taking the log of both sides | 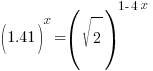 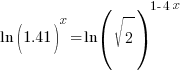 |
| Use the power rule for logarithms | 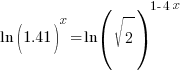 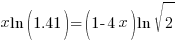 |
| Use the distributive law | 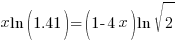 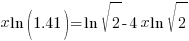 |
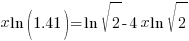 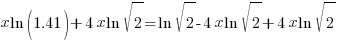 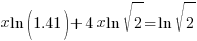 |
|
| Factor the common x | 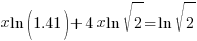 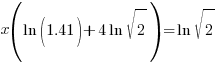 |
| Solve for x by dividing both sides by the factor in the parenthesis and simplify | 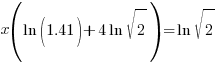 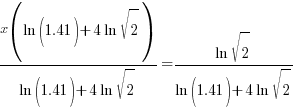 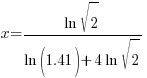 |
| The solution | 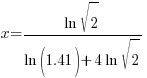 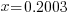 |
When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator. Here is an example of how you might enter it.
(ln (sqrt{2}))/(ln(1.41)+4 ln(sqrt{2}))
Here is a youtube video with a similar example.
Solve the Logarithmic Equation by the one to one property
Example:
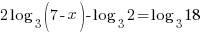
Solution:
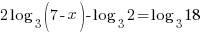 |
|
| Use the power rule and the quotient rule to condense to a single logarithm | 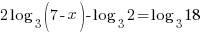 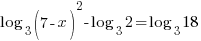 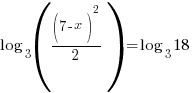 |
| Since both sides of the equation have the same log base the expressions inside the logarithms must be equal | 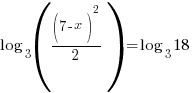 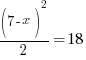 |
| Clear the denominator by multiplying by 2 on both sides and simplifying | 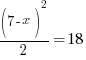 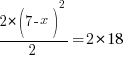 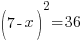 |
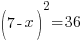 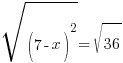 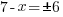 |
|
| Get x by itself by subtracting 7 on both sides | 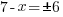 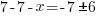 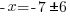 |
| Get x by itself by dividing both sides by negative 1 | 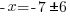 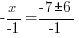 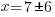 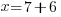 or or 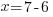 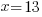 or or  |
| Check x=13 | 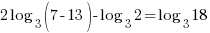 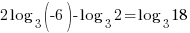 |
| Check x=1 | 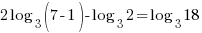 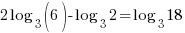 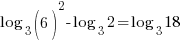 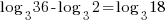 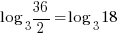 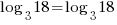 |
The solution to the equation is x=1.
Here is a youtube video that is similar.
Solving an Exponential Equation: Relating the Bases
Example: Solve the exponential equation.
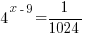
Solution:
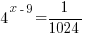 |
|
| Try to write both sides of the equation with the same base. Try 4 since there is a base of 4 on the left | 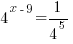 |
| Using a property of negative exponents move the base to the numerator | 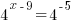 |
| Now that that the bases are the same the exponents must be equal | 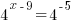
|
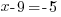
|
The solution the the exponential equation is 4.
Here is a youtube video with a similar example.
Rational Equation (no solution)
Example: Solve the rational equation.
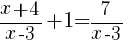
Solution:
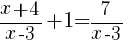
Since we are solving a rational equation we need to first find the restrictions (the values of x that cause the expression to be undefined).
To find the restrictions create an equation by setting each denominator equal to zero and solving.
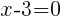
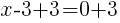
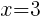
Having x=3 causes a zero in the denominator and the overall expression undefined. That makes 3 a restricted value .
With the restriction in mind we will solve the equation.
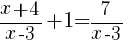 |
|
Multiply each side of the equation by the least common multiple of the denominators. For this equation the least common multiple is 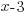 |
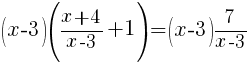 |
| Distribute the least common multiple to each term. | 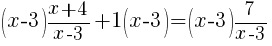 |
| Simplify by canceling the common factors. This should clear any denominators. | 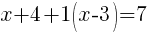 |
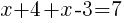 |
|
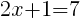 |
|
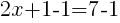 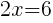 |
|
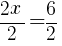 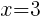 |
|
Video Example:
Higher Order Equation that reduces to a linear equation
Example: Solve the equation.
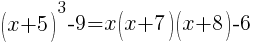
Solution:
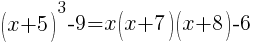 |
|
| Simplify both sides of the equation. On the left hand side, rewrite the exponent. On the right hand side, begin to simplify the multiplication. | 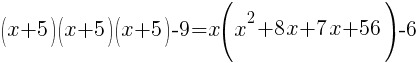 |
| Simplify both sides of the equation. On the left hand side, begin multiplying. On the right hand side, combine like terms. | 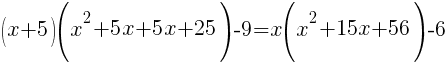 |
| Simplify both sides of the equation. On the left hand side, combine like terms. On the right hand side use the distributive property. | 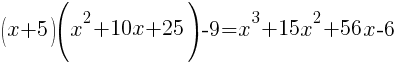 |
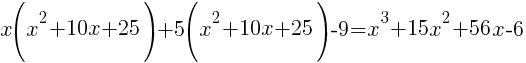 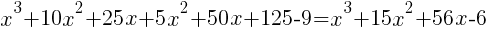 |
|
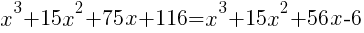 |
|
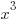 from each side. It cancels from each side. from each side. It cancels from each side. |
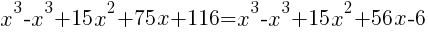 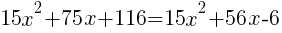 |
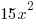 from each side. It cancels from each side. from each side. It cancels from each side. |
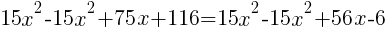 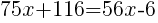 |
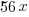 from each side and simplify. from each side and simplify. |
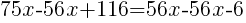 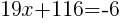 |
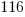 from each side and simplify. from each side and simplify. |
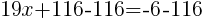 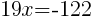 |
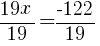 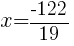 |
Quadratic in Form (U-substitution)
Example: Solve the equation.
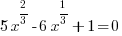
Solution:
The equation is similar to a quadratic. It has 3 terms and one exponent is twice the other. Since the equation is quadratic in form, use substitution to solve the equation.
Use the following substitution to rewrite the equation
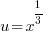
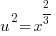
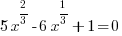 |
|
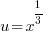 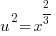 |
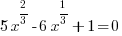 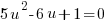 |
1) Factor the quadratic |
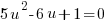 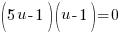 |
2) Apply the zero product property |
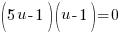 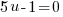 or or 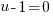 |
3) Solve each linear factor |
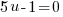 or or 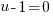 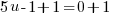 or or 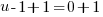 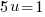 or or 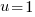 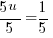 or or 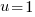 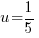 or or 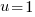 |
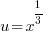 |
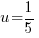 or or 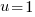 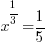 or or 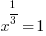
|
| Solve the equation with rational exponents. 1) Rewrite the rational exponents in radical form |
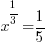 or or 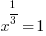 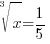 or or 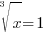 |
| Solve the equation with rational exponents. 2) Cancel the cube root by cubing both sides. 3) Simplify |
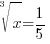 or or 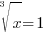 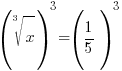 or or 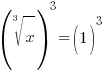 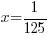 or or  |
The solution to 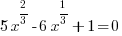 is
is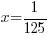 or
or  .
.
Here is a video with similar examples.
Forms of Linear Equations
Slope Intercept Form
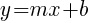
m is the slope of the line and 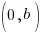 is the y-intercept
is the y-intercept
Point Slope Form
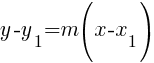
m is the slope of the line and 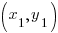 is a point on the line.
is a point on the line.
Standard Form of a Line