1.1 Linear Equations, Solving Equations

Rational Equation (no solution)

Example: Solve the rational equation.

{x+4}/{x-3}+1=7/{x-3}

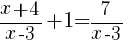
Solution:

{x+4}/{x-3}+1=7/{x-3}

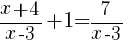
Since we are solving a rational equation we need to first find the restrictions (the values of x that cause the expression to be undefined).

To find the restrictions create an equation by setting each denominator equal to zero and solving.

x-3=0

x-3+3=0+3

x=3

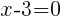
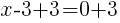
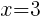
Having x=3 causes a zero in the denominator and the overall expression undefined.  That makes 3 a restricted value .

With the restriction in mind we will solve the equation.

 

The original equation
 {x+4}/{x-3}+1=7/{x-3}
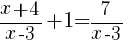Multiply each side of the equation by the least common multiple of the denominators.  For this equation the least common multiple is 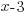x-3
(x-3)({x+4}/{x-3}+1)=(x-3)7/{x-3}
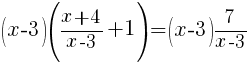Distribute the least common multiple to each term.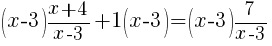
(x-3){x+4}/{x-3}+1(x-3)=(x-3)7/{x-3}
Simplify by canceling the common factors.  This should clear any denominators.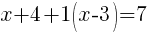
x+4+1(x-3)=7
Use the distributive property to simplify.
x+4+x-3=7
Simplify each side of the equation by combining like terms.
2x+1=7
Solve for x by getting x by itself on one side.  Start by subtracting 1 on both sides.
2x+1-1=7-1
2x=6
 Solve for x by getting x by itself on one side.  Next divide both sides by 2.
{2x}/2=6/2
x=3
Compare your solution to the restricted value.
Since the solution is the same as the restricted value we must exclude it as a solution.  Since all of the solutions have been excluded, there is no solution to the rational equation.

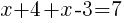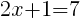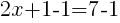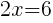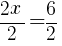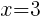Video Example: