Category Archives: 3.5 Graphing Techiques: Transformations
Transformation of Functions: Transforming the Square Root Function
Transformation of Functions: Horizontal and Vertical Reflections
Transformations of Functions: Vertical and Horizontal Shifts
Transformation of Functions: Vertical and Horizontal Stretch and Compression
Graphing by Transformations: Quadratic
Example: For the function below. Graph using transformations.
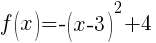
First we must examine the base function 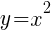
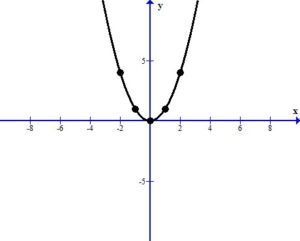
Graph using plotting points. We can use the standard set of x-values to find ordered pairs. Substitute the standard set of x-values into the base function to get the base graph.
| x | y |
|---|---|
| -2 | (-2)^2=4 |
| -1 | (-1)^2=1 |
| 0 | (0)^2=0 |
| 1 | (1)^2=1 |
| 2 | (2)^2=4 |
The graph below shows the points plotted and the line that connects them. The domain is 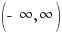 and the range is [
and the range is [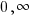 )
)
Analyze the transformations.
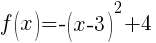
The -3 inside the square shifts the graph right 3 units.
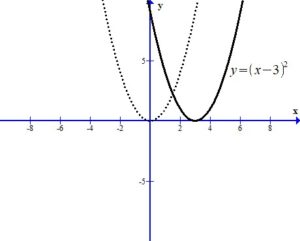
The – in the front of the base reflects the graph over the x-axis.
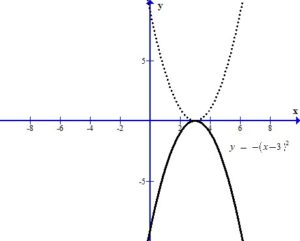
The +4 outside the square shifts the graph up 4 units.
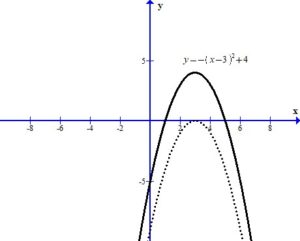
You can see the graph after the transformations.
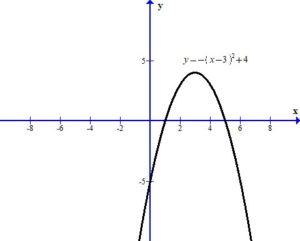
The domain is 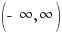 and the range is (
and the range is (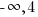 ]
]
Here is a video example of a transformation of a square function.
Graphing an Exponential Equation by Transformations
Example: For the function below. Graph using transformations. Find the y-intercept. State the horizontal asymptote and the domain and range.
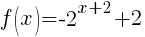
First we must examine the base function 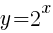
Graph using plotting points. We can use the standard set of x-values to find ordered pairs.
| x | y |
|---|---|
| -2 | 2^(-2)=1/4 |
| -1 | 2^(-1)=1/2 |
| 0 | 2^0=1 |
| 1 | 2^1=2 |
| 2 | 2^2=4 |
The graph below shows the points plotted and the line that connects them. This graph has a horizontal asymptote at y=0. The domain is 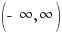 and the range is
and the range is 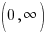
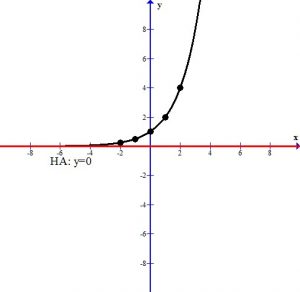
Analyze the transformations.
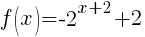
The +2 in the exponent shifts the graph left 2 units.
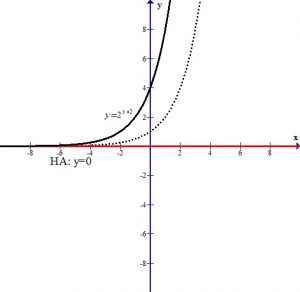
The – in the front of the base reflects the graph over the x-axis.
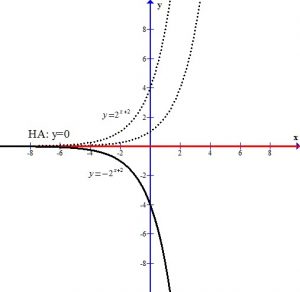
The +2 next to the base shifts the graph and the horizontal asymptote up two units.
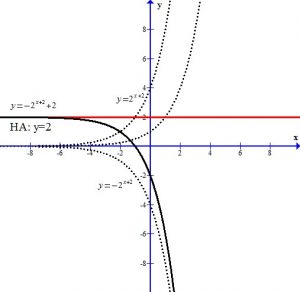
You can see the graph after the transformations.
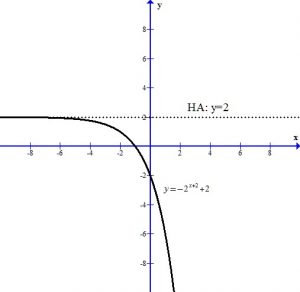
The horizontal asymptote is y=2. The domain is 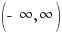 and the range is
and the range is 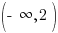
To find the y-intercept we let x=0.
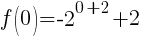
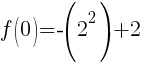
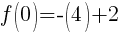
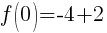
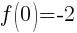
Thus the y-intercept is (0,-2)
Here is a youtube video with examples.