Example: For the function below. Graph using transformations. Find the y-intercept. State the horizontal asymptote and the domain and range.
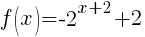
First we must examine the base function 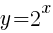
Graph using plotting points. We can use the standard set of x-values to find ordered pairs.
| x | y |
|---|---|
| -2 | 2^(-2)=1/4 |
| -1 | 2^(-1)=1/2 |
| 0 | 2^0=1 |
| 1 | 2^1=2 |
| 2 | 2^2=4 |
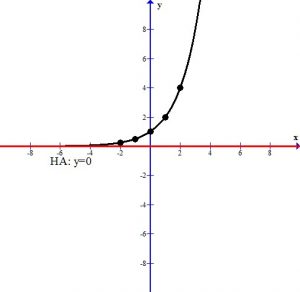
The graph below shows the points plotted and the line that connects them. This graph has a horizontal asymptote at y=0. The domain is 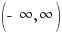 and the range is
and the range is 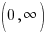
Analyze the transformations.
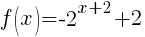
The +2 in the exponent shifts the graph left 2 units.
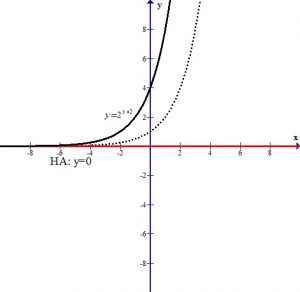
The – in the front of the base reflects the graph over the x-axis.
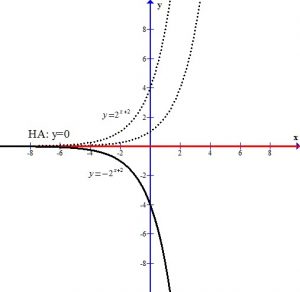
The +2 next to the base shifts the graph and the horizontal asymptote up two units.
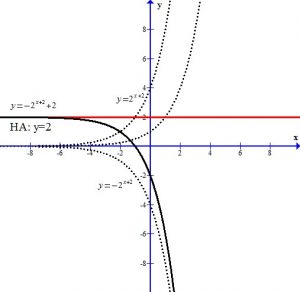
You can see the graph after the transformations.
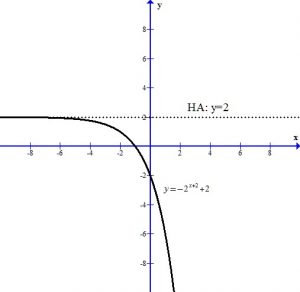
The horizontal asymptote is y=2. The domain is 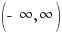 and the range is
and the range is 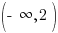
To find the y-intercept we let x=0.
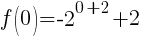
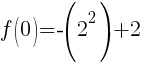
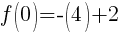
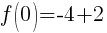
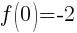
Thus the y-intercept is (0,-2)
Here is a youtube video with examples.
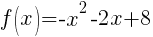
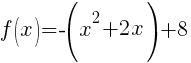
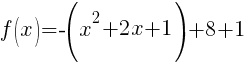
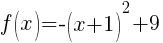
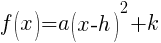
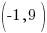 .
.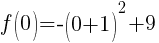
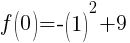
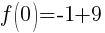
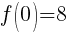
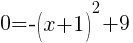
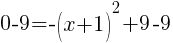
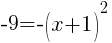
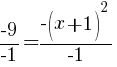
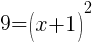
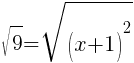
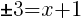
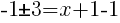
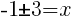
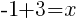 or
or 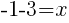
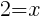 or
or 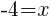
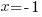 .
.
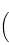
![- infty, 9 {}{]} - infty, 9 {}{]}](http://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_cf307bba3f49c962fc8d40a950c676b1.png) .
.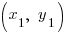 and B is
and B is 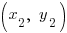
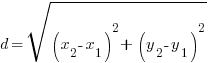
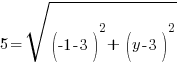
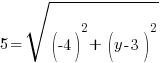
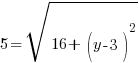
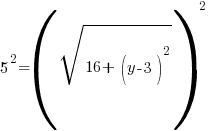
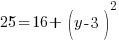
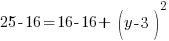
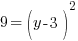
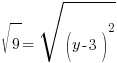
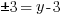
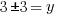
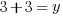 or
or 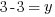
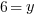 or
or 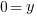
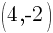 and point B is
and point B is 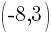
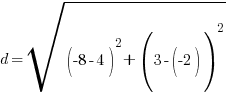
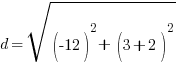
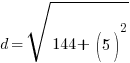
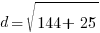
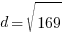
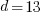
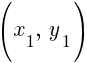 and B is
and B is 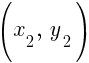
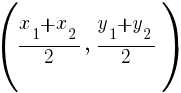
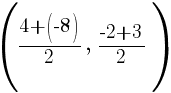
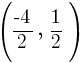
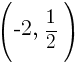
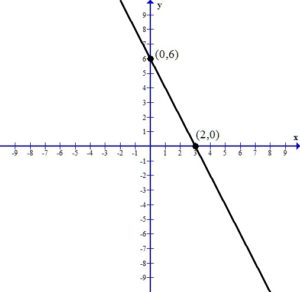
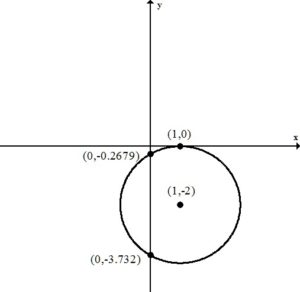
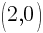 . Since every ordered pair on the x-axis has a y coordinate of zero we can let
. Since every ordered pair on the x-axis has a y coordinate of zero we can let 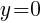 to find x-intercepts.
to find x-intercepts.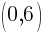 . Since every ordered pair on the y-axis has a x coordinate of zero we can let
. Since every ordered pair on the y-axis has a x coordinate of zero we can let 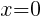 to find y-intercepts.
to find y-intercepts.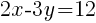
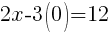
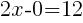
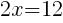
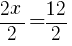
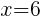
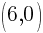
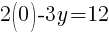
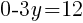
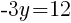
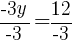
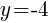
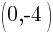
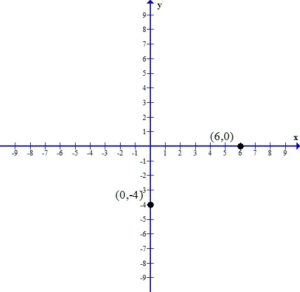
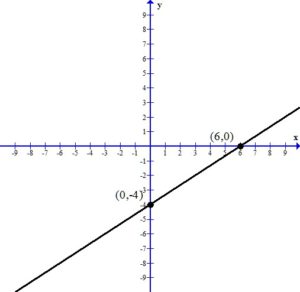
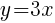
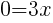
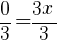
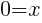
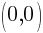
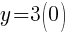
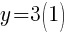
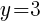
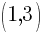
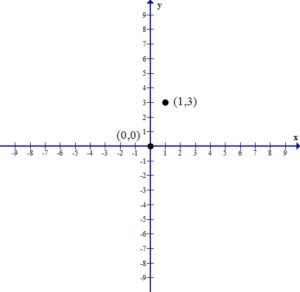
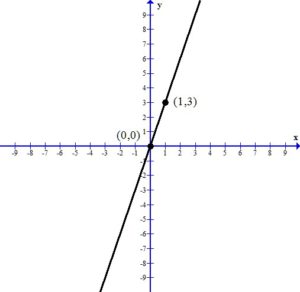
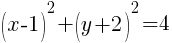
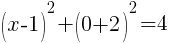
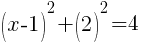
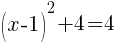
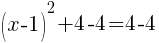
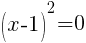
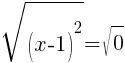
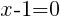
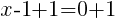
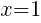
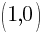
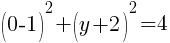
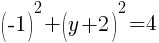
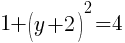
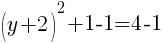
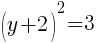
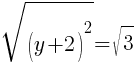
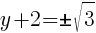
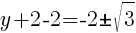
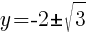
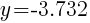 and
and 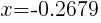
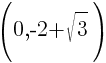 and
and 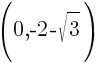
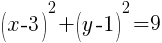
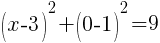
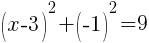
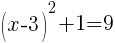
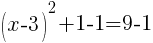
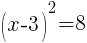
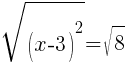
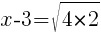
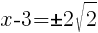
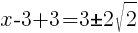
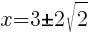
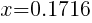 and
and 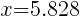
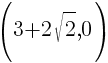 and
and 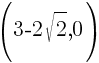
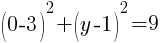
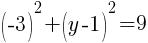
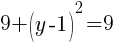
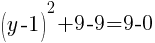
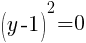
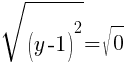
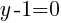
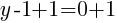
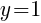
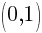 .
.