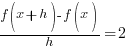Category Archives: 3.1 Functions
Add, Subtract, Multiply and Divide Functions
At 6:57 I made a mistake leaving off the negative on the 9. The domain of f/g is (-infinity,-3)U(-3, infinity)
Finding Domain of a Polynomial Function
Difference Quotient: Linear Function
Example: Find the difference quotient for 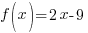
The Difference Quotient: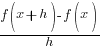
Solution:
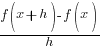 |
|
| Write the difference quotient for the given function | 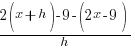 |
| Use the distributive property | 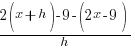 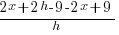 |
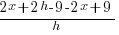 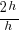 |
|
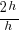 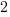 |
The difference quotient for the function 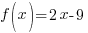 is
is