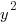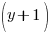Category Archives: Sullivan Chapter 5
Rational Function: Find Vertical Asymptotes and Holes (Rational Function has Common Factors
Rational Function: Find the Domain and Intercepts
Horizontal and Oblique Asymptotes (Case: degree of numerator is one more than the degree of the denominator)
Horizontal and Oblique Asymptotes (Case: degree of numerator is equal to the degree of the denominator)
Horizontal and Oblique Asymptotes (Case: degree of numerator is less than the degree of the denominator)
Properties of Rational Functions
Here is a handout with some of the significant definitions and properties related to rational functions.
Polynomial Equation (Solve by factoring with the grouping method)
Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 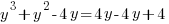 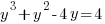 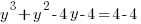 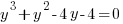 |
|
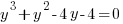 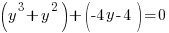 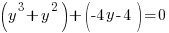 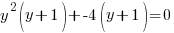 |
|
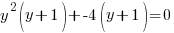 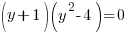 |
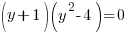 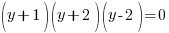 |
|
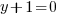 or or 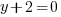 or or 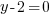 |
|
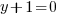 or or 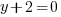 or or 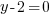 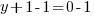 or or 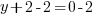 or or 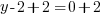 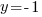 or or 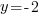 or or 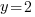 |
The solutions to the polynomial equation  are
are 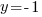 or
or 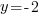 or
or 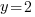 .
.
Solving Quadratic, Polynomial, and Rational Inequalities Graphically
Here is a worksheet to help you practice with polynomial and rational inequalities.
Solving Polynomial and Rational Inequalities Graphically
Here are the solutions to the worksheet above.
Solving Polynomial and Rational Inequalities Graphically Solutions updated