Category Archives: 5.2 The Real Zeros of a Polynomial Function
Polynomial Function: Finding Zeros and Write in Factored Form
Problem: Use the rational zeros theorem to find all real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
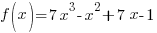
Since f is a polynomial function with integer coefficients use the rational zeros theorem to find the possible zeros.
The factors of the constant term, 1 are p.
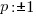
The factors of the leading coefficient, 7 are q.
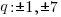
The possible rational zeros can be found by working out all of the possible combinations of p/q.
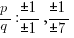
Simplifying these combinations give 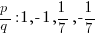
To test if any of these potential zeros are actual zeros, evaluate the function at these values.
| x | f(x) | f(x) |
|---|---|---|
| -1 | 7(-1)^3-(-1)^2+7(-1)-1 | -16 |
| -1/7 | 7(-1/7)^3-(-1/7)^2+7(-1/7)-1 | -2.041 |
| 1/7 | 7(1/7)^3-(1/7)^2+7(1/7)-1 | 0 |
| 1 | 7(1)^3-(1)^2+7(1)-1 | 12 |
This can be completed quickly using the ask feature in your calculator.




Since f(1/7) is zero, 1/7 is a zero of the function. Since the function has a zero of 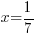 then the function has a factor of
then the function has a factor of 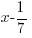
Use long division or synthetic division to to reduce the polynomial.
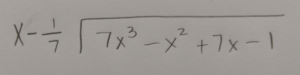 |
|
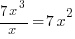 |
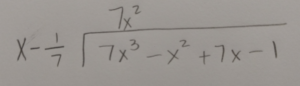 |
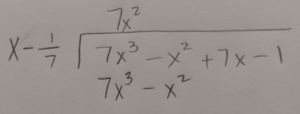 |
|
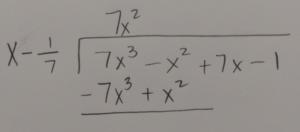 |
|
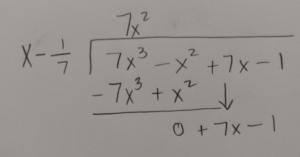 |
|
 |
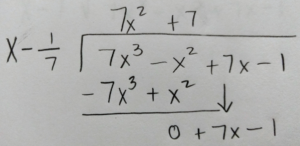 |
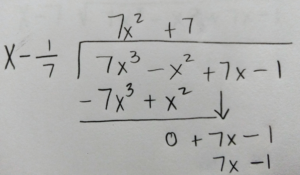 |
|
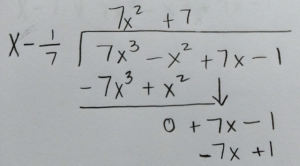 |
|
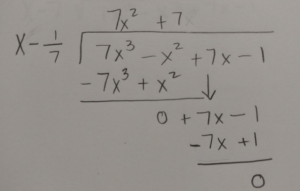 |
Write the function in factored form using the results of the long division.
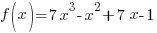
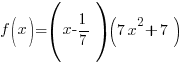
Factor completely.
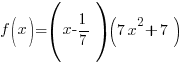
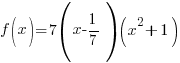
Intermediate Value Theorem
Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval. Approximate the zero to two decimal places.
![f(x)=9x^3+9x^2-9x+6; [-2,-1] f(x)=9x^3+9x^2-9x+6; [-2,-1]](http://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_8c3d8866a3f884f4b90f75e40f6be143.png)
Solution:
To determine if there is a zero in the interval use the Intermediate Value theorem. To use the Intermediate Value Theorem, the function must be continuous on the interval ![[-2,-1] [-2,-1]](http://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ffd21cf987ccbaa47dd393edf5d2bd04.png) . The function
. The function 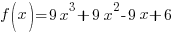 is a polynomial function and polynomial functions are defined and continuous for all real numbers.
is a polynomial function and polynomial functions are defined and continuous for all real numbers.
Evaluate the function at the endpoints and if there is a sign change. If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval. To evaluate the function at the endpoints, calculate 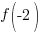 and
and 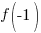 .
.
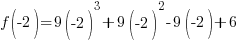
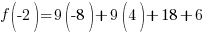
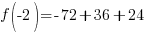
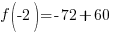
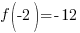
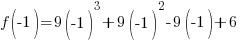
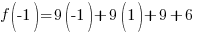
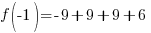
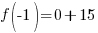
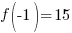
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.
We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.
| x | f(x) | f(x) |
|---|---|---|
| -2.0 | 9(-2)^3+9(-2)^2-9(-2)+6 | -12 |
| -1.9 | ||
| -1.8 | ||
| -1.7 | ||
| -1.6 | ||
| -1.5 | ||
| -1.4 | ||
| -1.3 | ||
| -1.2 | ||
| -1.1 | ||
| -1.0 | 9(-1)^3+9(-1)^2-9(-1)+6 | 15 |
Fill the table. There are functions in your calculator that make this easier.



| x | f(x) | f(x) |
|---|---|---|
| -2.0 | 9(-2)^3+9(-2)^2-9(-2)+6 | -12 |
| -1.9 | 9(-1.9)^3+9(-1.9)^2-9(-1.9)+6 | -6.141 |
| -1.8 | 9(-1.8)^3+9(-1.8)^2-9(-1.8)+6 | -1.128 |
| -1.7 | 9(-1.7)^3+9(-1.7)^2-9(-1.7)+6 | 3.093 |
| -1.6 | 9(-1.6)^3+9(-1.6)^2-9(-1.6)+6 | 6.576 |
| -1.5 | 9(-1.5)^3+9(-1.5)^2-9(-1.5)+6 | 9.375 |
| -1.4 | 9(-1.4)^3+9(-1.4)^2-9(-1.4)+6 | 11.544 |
| -1.3 | 9(-1.3)^3+9(-1.3)^2-9(-1.3)+6 | 13.137 |
| -1.2 | 9(-1.2)^3+9(-1.2)^2-9(-1.2)+6 | 14.208 |
| -1.1 | 9(-1.1)^3+9(-1.1)^2-9(-1.1)+6 | 14.811 |
| -1.0 | 9(-1)^3+9(-1)^2-9(-1)+6 | 15 |
Use the Intermediate Value Theorem again. Look for a sign change. Looking down the table, there is a sign change between -1.8 and -1.7. With this information we now know the zero is between these two values.
Repeat this process again with two decimal places between -1.8 and -1.7.


| x | f(x) | f(x) |
|---|---|---|
| -1.80 | 9(-1.8)^3+9(-1.8)^2-9(-1.8)+6 | -1.128 |
| -1.79 | 9(-1.79)^3+9(-1.79)^2-9(-1.79)+6 | -.6712 |
| -1.78 | 9(-1.78)^3+9(-1.78)^2-9(-1.78)+6 | -.2222 |
| -1.77 | 9(-1.77)^3+9(-1.77)^2-9(-1.77)+6 | .219 |
| -1.76 | 9(-1.76)^3+9(-1.76)^2-9(-1.76)+6 | .65242 |
| -1.75 | 9(-1.75)^3+9(-1.75)^2-9(-1.75)+6 | 1.0781 |
| -1.74 | 9(-1.74)^3+9(-1.74)^2-9(-1.74)+6 | 1.4962 |
| -1.73 | 9(-1.73)^3+9(-1.73)^2-9(-1.73)+6 | 1.9066 |
| -1.72 | 9(-1.72)^3+9(-1.72)^2-9(-1.72)+6 | 2.3096 |
| -1.71 | 9(-1.71)^3+9(-1.71)^2-9(-1.71)+6 | 2.705 |
| -1.70 | 9(-1.7)^3+9(-1.7)^2-9(-1.7)+6 | 3.093 |
Use the Intermediate Value Theorem. Look for a sign change. Looking down the table, there is a sign change between -1.78 and -1.77. With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.
Remainder Theorem and Factor Theorem
Problem: Use the remainder theorem to find the remainder when f(x) is divided by 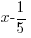 . Then use the factor theorem to determine whether
. Then use the factor theorem to determine whether 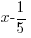 is a factor of f(x).
is a factor of f(x).
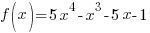
Solution:
The Remainder Theorem: Let f be a polynomial function. If 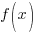 is divided by
is divided by 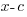 , then the remainder is
, then the remainder is 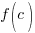 .
.
The remainder theorem gives a way to find the remainder without performing the division. The remainder when dividing by 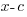 is
is 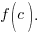 Calculate
Calculate 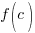 to find the remainder where c is the zero of the factor
to find the remainder where c is the zero of the factor 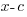 .
.
For the example above, f(x) is divided by 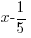 . The zero of the factor can be found by setting the factor equal to zero and solve.
. The zero of the factor can be found by setting the factor equal to zero and solve.
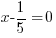
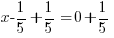
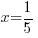
Use 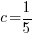 and calculate
and calculate 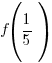 .
.
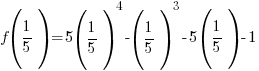
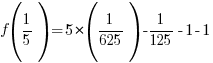
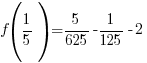
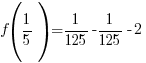
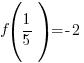
The remainder when f(x) is divided by 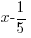 is -2.
is -2.
Factor Theorem: Let f be a polynomial function. Then 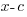 is a factor of f(x) if and only if
is a factor of f(x) if and only if 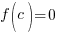 .
.
This theorem gives of the result that if 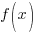 is divided by
is divided by 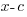 and the remainder is zero, then
and the remainder is zero, then 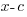 is a factor of f.
is a factor of f.
For the example above, the remainder when f(x) is divided by 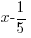 is -2. Since the remainder is not zero
is -2. Since the remainder is not zero 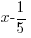 is not a factor.
is not a factor.