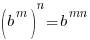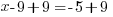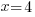Category Archives: 5.1 Exponential Functions
Exponential Equations: Same Base
Application: Exponential Growth
Graphing Exponential Functions (Base e)
Graphing an Exponential Function (Base Function)
Exponents: Simplify
Example: Rewrite the expression in the form 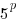 where p is an algebraic expression.
where p is an algebraic expression.
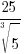
Solution:
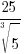 |
|
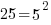 |
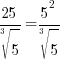 |
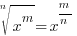 . For this example . For this example 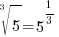 |
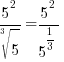 |
Quotient Rule for Exponents 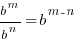 |
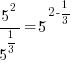 |
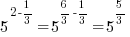 |
Periodic and Continuous Compound Interest
Solve an Exponential Equation: Relating the Bases
Problem: Solve the exponential equation.
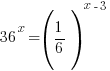
Solution:
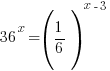 |
|
The bases of the exponents on each side of the equation can be made the same. 36 can be written as 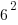 and and 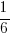 can be written as can be written as 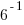 |
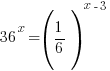 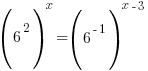 |
|
Use the power rule for exponents to multiply the exponents. |
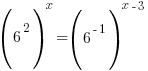 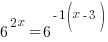 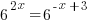 |
| Exponential functions are one-to-one thus giving us the property that if the bases are the same the exponents are equal. If 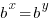 then then 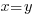 |
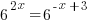 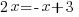 |
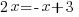 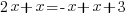 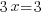
|
|
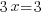 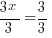  |
|
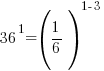 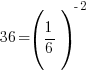 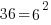 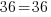 |
The solution to the equation 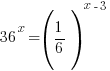 is
is  .
.
Here is a video example of a similar type of problem.
Solving an Exponential Equation: Relating the Bases
Example: Solve the exponential equation.
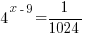
Solution:
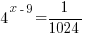 |
|
| Try to write both sides of the equation with the same base. Try 4 since there is a base of 4 on the left | 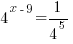 |
| Using a property of negative exponents move the base to the numerator | 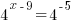 |
| Now that that the bases are the same the exponents must be equal | 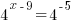
|
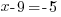
|
The solution the the exponential equation is 4.
Here is a youtube video with a similar example.
Graphing an Exponential Equation by Transformations
Example: For the function below. Graph using transformations. Find the y-intercept. State the horizontal asymptote and the domain and range.
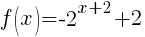
First we must examine the base function 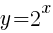
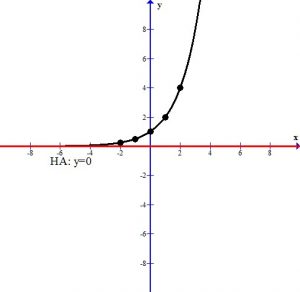
Graph using plotting points. We can use the standard set of x-values to find ordered pairs.
| x | y |
|---|---|
| -2 | 2^(-2)=1/4 |
| -1 | 2^(-1)=1/2 |
| 0 | 2^0=1 |
| 1 | 2^1=2 |
| 2 | 2^2=4 |
The graph below shows the points plotted and the line that connects them. This graph has a horizontal asymptote at y=0. The domain is 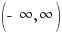 and the range is
and the range is 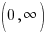
Analyze the transformations.
The +2 in the exponent shifts the graph left 2 units.
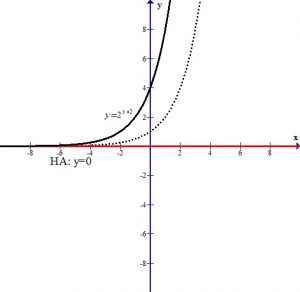
The – in the front of the base reflects the graph over the x-axis.
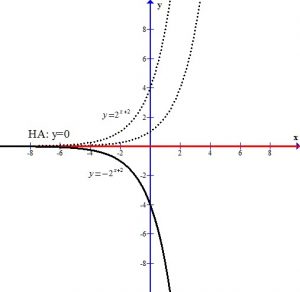
The +2 next to the base shifts the graph and the horizontal asymptote up two units.
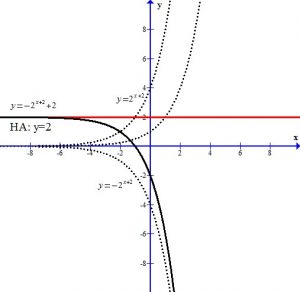
You can see the graph after the transformations.
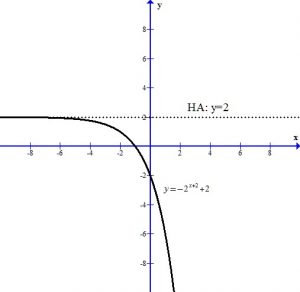
The horizontal asymptote is y=2. The domain is 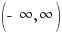 and the range is
and the range is 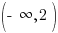
To find the y-intercept we let x=0.
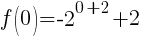
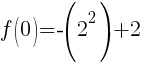
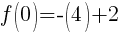
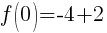
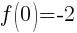
Thus the y-intercept is (0,-2)
Here is a youtube video with examples.