2.2 Lines, 2.4 Parallel and Perpendicular Lines, Finding the Equation of a Line

Finding the equation of a line perpendicular to another line

Example: Write the equation of a line in point-slope form passing through the point 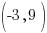(-3,9) and perpendicular to the line whose equation is y={6/5}x+9/5.

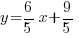Solution:

Use the point-slope formula of the line to start building the line.  m represents the slope of the line and 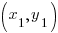(x_1,y_1) is a point on the line.

Point-slope formula: 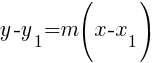y-y_1 = m(x-x_1)

Although the slope of the line is not given, the slope can be deducted from the line being perpendicular to 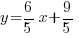y={6/5}x+9/5.

Perpendicular lines have negative reciprocal slopes.  Since the slope of the given line is 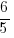6/5, the slope of the perpendicular line -5/6.

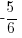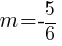m=-{5/6} and  (-3,9)

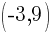
Substitute the values into the point-slope formula.

y-9 = {-5/6}(x-(-3))

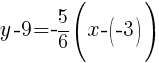
The point-slope form of the line is as follows.

y-9 = {-5/6}(x+3)

 

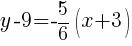
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope intercept form)

Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope standard form)

Example: Find the equation of a line perpendicular to the x-axis.

Example: Find the equation of a line perpendicular to the x-axis and perpendicular to the y-axis.