Example: Find the equation of a line in slope intercept form given the line passes through the two points 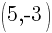 and
and 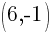 .
.
Solution:
First find the slope of the line.
Choose one of the points to be 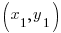 and choose the other point to be
and choose the other point to be 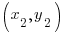 .
.
I will choose 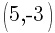 to be
to be 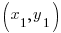 and choose
and choose 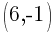 to be
to be 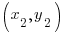 .
.
Substitute these values into the slope formula and simplify.
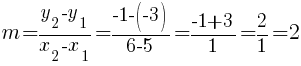
The slope of the line containing the points 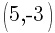 and
and 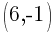 is
is 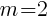 .
.
Then, use the point-slope formula of the line to start building the line. m represents the slope of the line and you can use 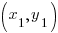 or
or 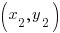 as the point on the line.
as the point on the line.
Point-slope formula: 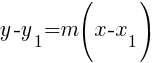
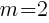 and
and 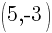
Substitute the values into the formula.
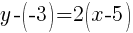
Since the instructions ask to write the equation in slope intercept form 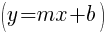 we will simplify and write the equation with y by itself on one side.
we will simplify and write the equation with y by itself on one side.
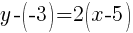
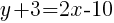
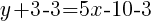
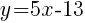
The equation of a line in slope intercept form passing through the two points 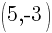 and
and 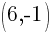 is
is 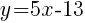 .
.