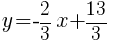Example: Find the equation of a line in slope intercept form given the slope of the line is 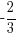 and the line passes through the point
and the line passes through the point 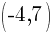
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 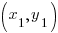 is a point on the line.
is a point on the line.
Point-slope formula: 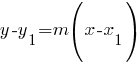
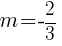 and
and 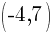
Substitute the values into the formula.
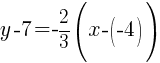
Since the instructions ask to write the equation in slope intercept form 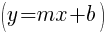 we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
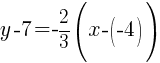
![3(y-7) = 3[-{2/3}(x+4)] 3(y-7) = 3[-{2/3}(x+4)]](http://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980_0233a6f7265fc4d6a65d52d25e31bbd1.png) (Multiply by LCM)
(Multiply by LCM)
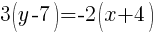 (Cancel Denominator)
(Cancel Denominator)
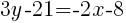
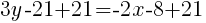
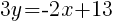
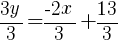
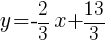
The equation of a line in slope intercept form with a slope of 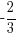 and passing through the point
and passing through the point 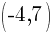 is
is