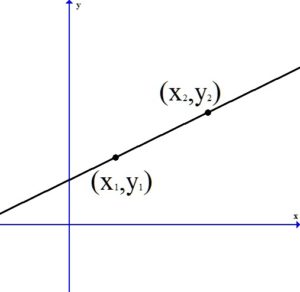
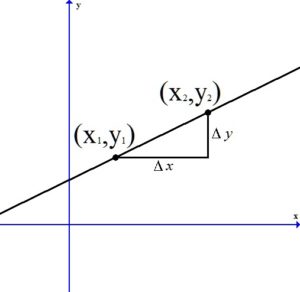
Given two points on the line 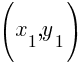 and
and 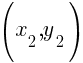 , you can calculate the slope of a line by the following formula.
, you can calculate the slope of a line by the following formula.
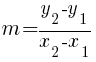
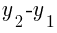 is also know as
is also know as 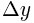 or “the change in y.”
or “the change in y.”
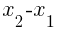 is also know as
is also know as 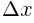 or “the change in x.”
or “the change in x.”
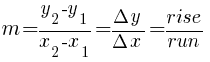
Example: Calculate the slope of the line containing the points 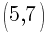 and
and 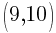 .
.
Solution: Choose one of the points to be 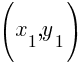 and choose the other point to be
and choose the other point to be 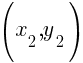 .
.
I will choose 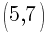 to be
to be 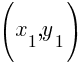 and choose
and choose 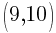 to be
to be 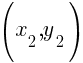 .
.
Substitute these values into the slope formula and simplify.
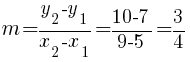
The slope of the line containing the points 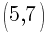 and
and 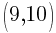 is
is 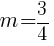 .
.
Example: Calculate the slope of the line containing the points 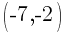 and
and 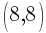 .
.
Solution: Choose one of the points to be 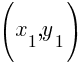 and choose the other point to be
and choose the other point to be 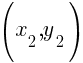 .
.
I will choose 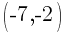 to be
to be 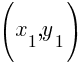 and choose
and choose 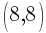 to be
to be 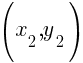 .
.
Substitute these values into the slope formula and simplify.
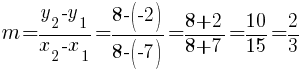
The slope of the line containing the points 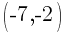 and
and 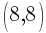 is
is 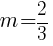 .
.
Example: Finding the slope with the formula.
https://www.youtube.com/watch?v=1Cm7hjMUsrQ
Example: Finding the slope with the formula.
Example: Finding the slope from the graph.