5.5 Applications of Exponential and Logarithmic Functions, 6.7 Financial Models, Applications of Exponential Functions

Application of Exponential Functions: Doubling Time

Example:

How long does it take for an investment to double if it is invested at 18% compounded continuously?

Solution:

Since this question involve continuous compound interest, we will use the associated formula.

A=Pe^{rt}

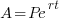
We are given that the interest rate is 18% or 0.18.  This tells me that when r=0.18 Since we are looking for the doubling time, A will be 2 times P.  I can write that in symbols A=2P.

Substitute these values into the continuous compound formula and solve for the interest rate.

Continuous compound formula
A=Pe^{rt}
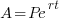Substitute the values of r and A into the formula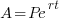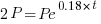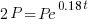
A=Pe^{rt}
2P=Pe^{0.18*t}
2P=Pe^{0.18t}
Solve for t by dividing both sides by P and simplifying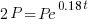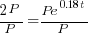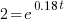
2P=Pe^{0.18t}
{2P}/P={Pe^{0.18t}}/P
2=e^{0.18t}
Solve for t by taking the log of both sides.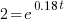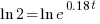
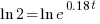2=e^{0.18t}
ln 2=ln e^{0.18t}
Solve for t by using the power rule and simplifying
ln 2=ln e^{0.18t}
ln 2=0.18t ln e
ln 2=0.18t (1)
ln 2=0.18t
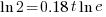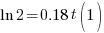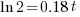Solve for t by dividing both sides by 0.18 and simplifying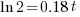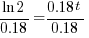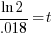
ln 2=0.18t
{ln 2}/0.18={0.18t}/0.18
{ln 2}/.018=t
Find the value in the calculator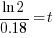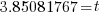
{ln 2}/0.18=t
3.85081767=t
Write the answer rounded to two decimal places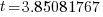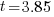
t=3.85081767
t=3.85

It will take 3.85 years to double your money when interest is compounded continuously at 18%.

If you need to write this in years and months, you will need to convert the 0.85 to months.  Since there are 12 months in a year, multiply 0.85 by 12 to get 10.2.  I will round to the nearest months to get 10.

It will take 3 years and 10 months to double your money when interest is compounded continuously at 18%.

Here is a video that is similar except that you are looking for the investment to triple.