Example: The half life of radium is 1690 years. If 50 grams are present now, how much will be present in 630 years?
Solution: There is a two part process to this problem. Part 1: Use some of the information to find the decay rate of radium. Part 2: Answer the question using the rest of the given information.
Part 1: Find the decay rate of radium.
Since we are using an exponential model for this problem we should be clear on the parts of the exponential decay model.
Exponential Decay Model
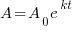
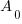 is the initial amount
is the initial amount
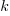 is the decay rate
is the decay rate
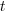 is the time
is the time
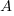 is the amount after t time has passed
is the amount after t time has passed
Since radium has a half life of 1690 years, we know that after 1690 years there will be half of the initial amount of radium left. This allows me to establish a relationship between the initial amount and the amount after 1690. The amount after 1690 year is half of the initial amount. 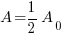 when the
when the 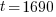 .
.
Substitute these values into the exponential decay formula and solve for k.
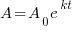 |
|
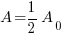 and and  |
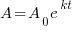 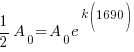 |
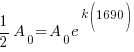 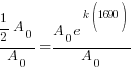 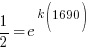 |
|
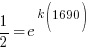 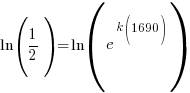 |
|
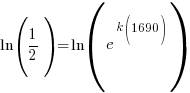 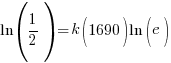 |
|
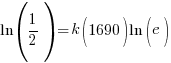 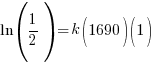 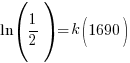 |
|
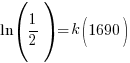 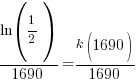 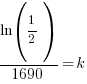 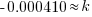 |
Using only the information about radium having a half-life of 1690 years I have found the decay rate for radium.
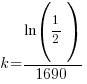
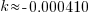
Note: Although I have put an approximation for k here, try not to round until the very last step.
Part 2: Answer the question using the rest of the given information.
Given information: If 50 grams are present now, how much will be present in 630 years?
With this information I can identify the initial amount of radium as 50 grams and the time to be 630 years. Symbolically that is 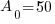 when the
when the 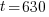 . Substitute the given information and the decay rate k found in part 1 to the exponential decay formula.
. Substitute the given information and the decay rate k found in part 1 to the exponential decay formula.
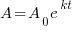 |
|
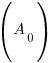 , time (t), and the decay rate (k). , time (t), and the decay rate (k).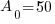 , , 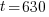 , and , and 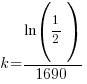 |
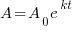 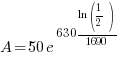 |
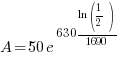 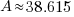 |
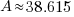
38.615 grams will be present 630 years later is 50 grams are present initially.
Here is a video example that is similar to the above example and it shows how to enter information in the calculator.