Problem:
A 28 inch wire is to be cut. One piece is to be bent into the shape of a square, whereas the other piece is the bent into the shape of a rectangle whose length is twice the width. Find the width of the rectangle that will minimize the total area.
Solution:
First draw a picture of the shapes the wire will make and label the sides.
The square has equal sides. Label the side as an unknown quantity x.
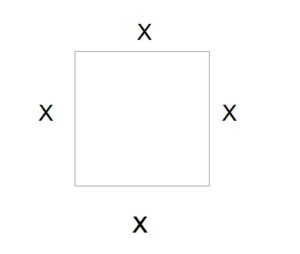
The perimeter of the square is 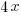 and the area of the square is
and the area of the square is 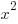 .
.
The rectangle described as a length that is twice the width. Label the sides as y and 2y.

The perimeter of the rectangle is 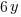 and the area of the rectangle is
and the area of the rectangle is 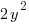 .
.
Since the 28 inch piece of wire will be cut and used to form the square and rectangle the total perimeter of the two shapes is 28 inches.
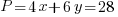
The total area is to be minimized.
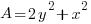
To minimize the area there must be only one variable in the expression. Use the perimeter equation to reduce the number of variables.
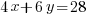 |
|
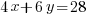 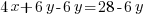 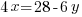 |
|
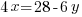 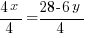 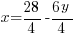 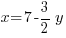 |
Substitute into the area expression to reduce from having two variables to have one variable.
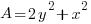 |
|
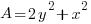 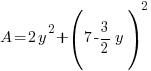 |
|
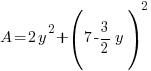 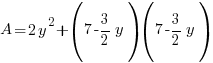 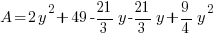 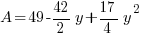 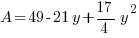 |
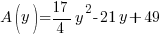 is in the form of a quadratic function. The graph of a quadratic function is a parabola. This quadratic function has a leading coefficient of
is in the form of a quadratic function. The graph of a quadratic function is a parabola. This quadratic function has a leading coefficient of 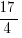 and since it is positive means that the parabola is opening up.
and since it is positive means that the parabola is opening up.
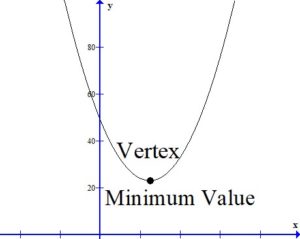
Find the vertex to find the minimum value.
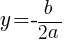 |
|
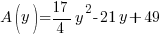 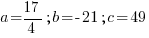 |
|
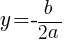 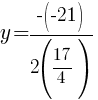 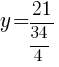 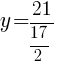 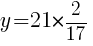 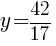 |
|
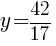 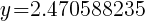 |
Round to the nearest tenth and 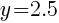 .
.
The total area of the square and rectangle is minimized when the width of the rectangle is 2.5 inches.