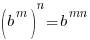Problem: Solve the exponential equation.
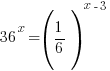
Solution:
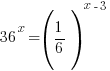 |
|
The bases of the exponents on each side of the equation can be made the same. 36 can be written as 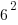 and and 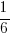 can be written as can be written as 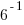 |
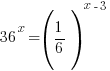 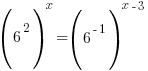 |
|
Use the power rule for exponents to multiply the exponents. |
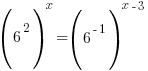 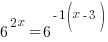 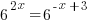 |
| Exponential functions are one-to-one thus giving us the property that if the bases are the same the exponents are equal. If 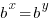 then then 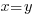 |
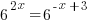 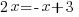 |
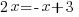 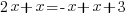 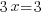
|
|
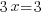 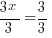  |
|
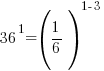 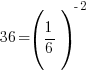 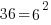 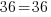 |
The solution to the equation 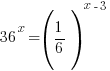 is
is  .
.
Here is a video example of a similar type of problem.