Example:

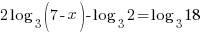
Solution:

 

The logarithmic equation
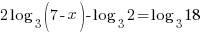Use the power rule and the quotient rule to condense to a single logarithm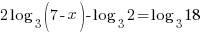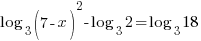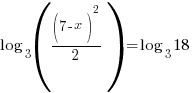
Since both sides of the equation have the same log base the expressions inside the logarithms must be equal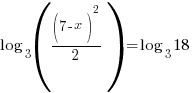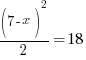
Clear the denominator by multiplying by 2 on both sides and simplifying
Get rid of the square by square rooting both sides and simplifying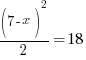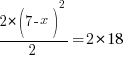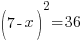
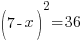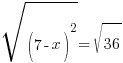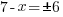Get x by itself by subtracting 7 on both sides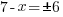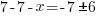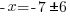
Get x by itself by dividing both sides by negative 1	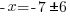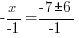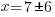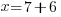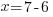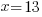or or
Check x=13	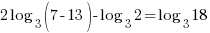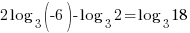Log of a negative is undefined.  Exclude this solution.
Check x=1	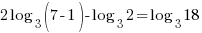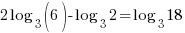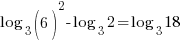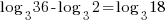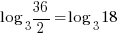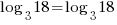Keep this solution.

The solution to the equation is x=1.

Here is a youtube video that is similar.