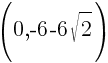2.2 Circles, 2.3 Circles, Finding Intercepts of a Circle, Intercpets

Finding the Intercepts of a Circle (4 Intercepts)

An x-intercept is where the graph touches or crosses the x-axis.

A y-intercept is where the graph touches of crosses the y-axis.

To find an x-intercept: Let y=0 and solve for x.

To find an y-intercept: Let x=0 and solve for y.

 

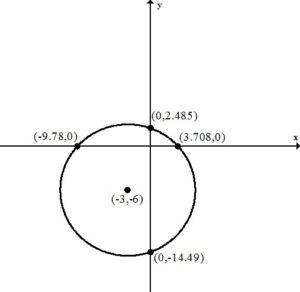
Example:  Find the intercepts of the circle for the given equation.

(x+3)^2+(y+6)^2=81

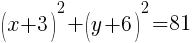
Solution:

To find an x-intercept, let y=0 and solve for x.

(x+3)^2+(y+6)^2=81

(x+3)^2+(0+6)^2=81

(x+3)^2+(6)^2=81

(x+3)^2+36=81

(x+3)^2+36-36=81-36

(x+3)^2=45

sqrt{(x+3)^2}=sqrt{45}

x+3=pm sqrt{9*5}

x+3=pm 3sqrt{5}

x+3-3=-3 pm 3sqrt{5}

x=-3 pm 3sqrt{5}

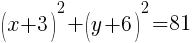
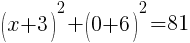
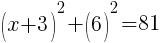
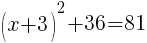
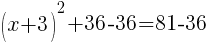
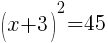
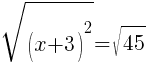
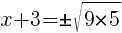
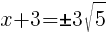
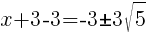
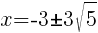
Approximately 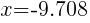x=-9.708 and x=3.708

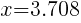
This equation has two x-intercepts. 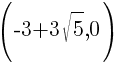(-3 + 3sqrt{5},0) and (-3 - 3sqrt{5},0)

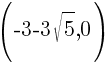
To find a y-intercept, let x=0 and solve for y.

(x+3)^2+(y+6)^2=81

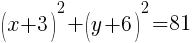
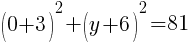
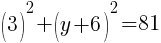
(0+3)^2+(y+6)^2=81

(3)^2+(y+6)^2=81

9+(y+6)^2=81

(y+6)^2+9-9=81-9

(y+6)^2=72

sqrt{(y+6)^2}=sqrt{72}

y+6=pm sqrt{36*2}

y+6=pm 6sqrt{2}

y+6-6=-6 pm 6sqrt{2}

y=-6 pm 6sqrt{2}

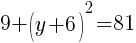
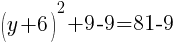
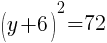
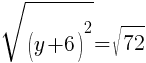
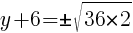
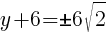
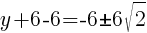
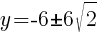
Approximately 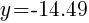y=-14.49 and x=2.485

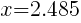
This equation has two y-intercepts. 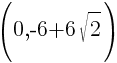(0,-6 + 6sqrt{2}) and (0,-6 - 6sqrt{2})