A circle is the collection of points that are equidistant to a center point. The distance is the radius denoted r. The center is denoted 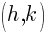 .
.
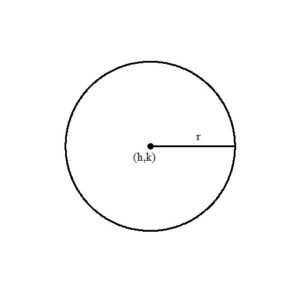
The standard form of an equation of a circle is 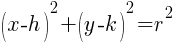 where r is the radius and
where r is the radius and 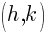 is the center.
is the center.
Example: Find the center and the radius from the given equation.
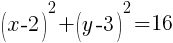
Solution: If you line up the standard form of a circle with the equation given you can determine the center and the radius.
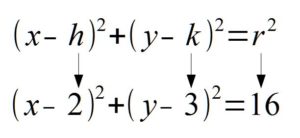
In the binomial with x, the number after the minus sign is h. Thus, 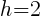 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 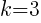 . The
. The 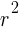 lines up with 16. So
lines up with 16. So 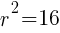 which means
which means 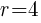 .
.
This is the equation of a circle with a center of 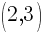 and a radius of
and a radius of 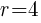 .
.
Example: Find the center and the radius from the given equation.
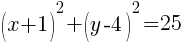
Solution: Notice that one of the binomials has a + instead of the – that is in the standard form of the circle. Rewrite the addition as subtraction.
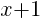 is the same as
is the same as 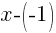 .
.
The rewritten equation is as follows.
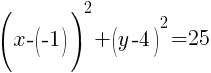
Then, if you line up the standard form of a circle with the equation given you can determine the center and the radius.
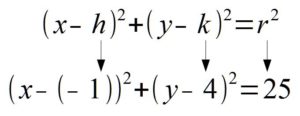
In the binomial with x, the number after the minus sign is h. Thus, 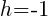 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 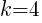 . The
. The 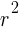 lines up with 25. So
lines up with 25. So 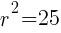 which means
which means 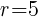 .
.
This is the equation of a circle with a center of 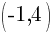 and a radius of
and a radius of 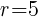 .
.
Example: Find the center and the radius from the given equation.
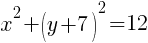
Solution: Notice that one of the binomials has a + instead of the – that is in the standard form of the circle. Rewrite the addition as subtraction.
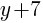 is the same as
is the same as 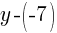 .
.
The other binomial doesn’t have any number added or subtracted. We can rewrite this by subtracting zero.
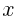 is the same as
is the same as 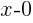 .
.
The rewritten equation is as follows.
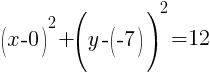
Then, if you line up the standard form of a circle with the equation given you can determine the center and the radius.
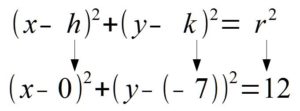
In the binomial with x, the number after the minus sign is h. Thus, 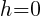 . In the binomial with y, the number after the minus sign is k. Thus,
. In the binomial with y, the number after the minus sign is k. Thus, 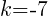 . The
. The 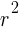 lines up with 25. So
lines up with 25. So 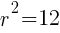 which means
which means 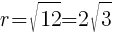 .
.
This is the equation of a circle with a center of 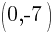 and a radius of
and a radius of 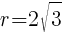 .
.