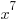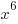Example: Determine if the function is even, odd, or neither.

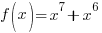
Background Knowledge:

For a function to be even it must fit the following definition.

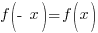
In words, this means that 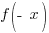must equal the same expression as the original function.

For a function to be odd it must fit the following definition.

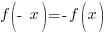
In words, this means that 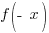must equal the opposite expression as the original function.

We will calculate 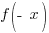  for the given function and determine if it fits either definition.

Solution:

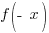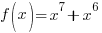We will calculate   for and determine if it fits either definition.

Calculate
Simplify . Group the negatives. Since there are an odd number of negatives multiplied the product is negative. Group the x’s.  Since the bases are the same, 7 x’s multiplied equals
Simplify . Group the negatives. Since there are an even number of negatives multiplied the product is positive. Group the x’s.  Since the bases are the same, 6 x’s multiplied equals

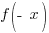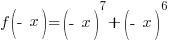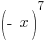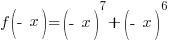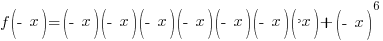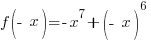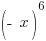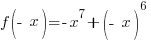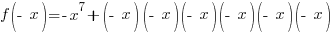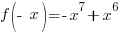Is the function even? No, 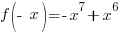 is not the same as the original function.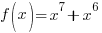

Is the function odd? No, 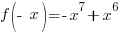is not the opposite of the original function.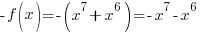

This function is not even or odd so we categorize it as “neither.”

YouTube Videos