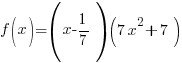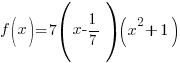Problem: Use the rational zeros theorem to find all real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
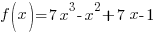
Since f is a polynomial function with integer coefficients use the rational zeros theorem to find the possible zeros.
The factors of the constant term, 1 are p.
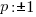
The factors of the leading coefficient, 7 are q.
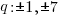
The possible rational zeros can be found by working out all of the possible combinations of p/q.
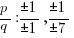
Simplifying these combinations give 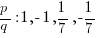
To test if any of these potential zeros are actual zeros, evaluate the function at these values.
| x | f(x) | f(x) |
|---|---|---|
| -1 | 7(-1)^3-(-1)^2+7(-1)-1 | -16 |
| -1/7 | 7(-1/7)^3-(-1/7)^2+7(-1/7)-1 | -2.041 |
| 1/7 | 7(1/7)^3-(1/7)^2+7(1/7)-1 | 0 |
| 1 | 7(1)^3-(1)^2+7(1)-1 | 12 |
This can be completed quickly using the ask feature in your calculator.




Since f(1/7) is zero, 1/7 is a zero of the function. Since the function has a zero of 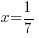 then the function has a factor of
then the function has a factor of 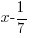
Use long division or synthetic division to to reduce the polynomial.
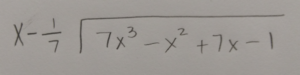 |
|
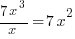 |
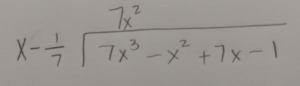 |
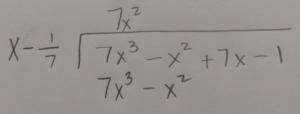 |
|
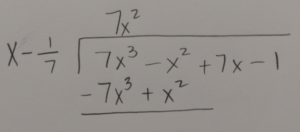 |
|
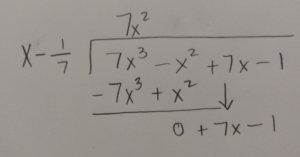 |
|
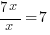 |
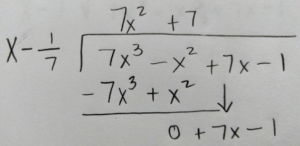 |
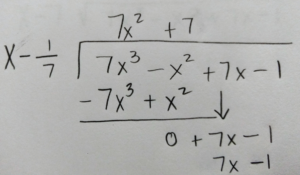 |
|
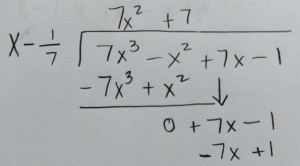 |
|
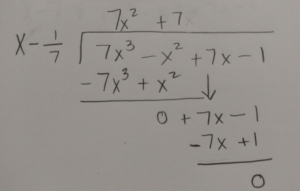 |
Write the function in factored form using the results of the long division.
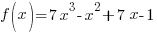
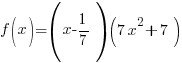
Factor completely.