Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval.  Approximate the zero to two decimal places.

Solution:

To determine if there is a zero in the interval use the Intermediate Value theorem.  To use the Intermediate Value Theorem, the function must be continuous on the interval .  The function 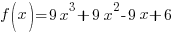 is a polynomial function and polynomial functions are defined and continuous for all real numbers.

Evaluate the function at the endpoints and if there is a sign change.  If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval.  To evaluate the function at the endpoints, calculate 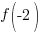  and .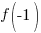

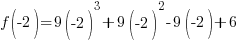
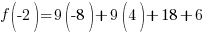
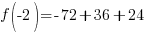
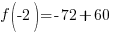
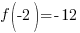
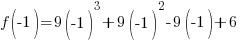
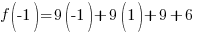
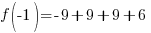
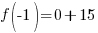
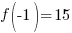
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.

We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.

x	f(x)	f(x)
-2.0	9(-2)^3+9(-2)^2-9(-2)+6	-12
-1.9
-1.8
-1.7
-1.6
-1.5
-1.4
-1.3
-1.2
-1.1
-1.0	9(-1)^3+9(-1)^2-9(-1)+6	15

Fill the table.  There are functions in your calculator that make this easier.

x	f(x)	f(x)
-2.0	9(-2)^3+9(-2)^2-9(-2)+6	-12
-1.9	9(-1.9)^3+9(-1.9)^2-9(-1.9)+6	-6.141
-1.8	9(-1.8)^3+9(-1.8)^2-9(-1.8)+6	-1.128
-1.7	9(-1.7)^3+9(-1.7)^2-9(-1.7)+6	3.093
-1.6	9(-1.6)^3+9(-1.6)^2-9(-1.6)+6	6.576
-1.5	9(-1.5)^3+9(-1.5)^2-9(-1.5)+6	9.375
-1.4	9(-1.4)^3+9(-1.4)^2-9(-1.4)+6	11.544
-1.3	9(-1.3)^3+9(-1.3)^2-9(-1.3)+6	13.137
-1.2	9(-1.2)^3+9(-1.2)^2-9(-1.2)+6	14.208
-1.1	9(-1.1)^3+9(-1.1)^2-9(-1.1)+6	14.811
-1.0	9(-1)^3+9(-1)^2-9(-1)+6	15

Use the Intermediate Value Theorem again.  Look for a sign change.  Looking down the table, there is a sign change between -1.8 and -1.7.  With this information we now know the zero is between these two values.

Repeat this process again with two decimal places between -1.8 and -1.7.

x	f(x)	f(x)
-1.80	9(-1.8)^3+9(-1.8)^2-9(-1.8)+6	-1.128
-1.79	9(-1.79)^3+9(-1.79)^2-9(-1.79)+6	-.6712
-1.78	9(-1.78)^3+9(-1.78)^2-9(-1.78)+6	-.2222
-1.77	9(-1.77)^3+9(-1.77)^2-9(-1.77)+6	.219
-1.76	9(-1.76)^3+9(-1.76)^2-9(-1.76)+6	.65242
-1.75	9(-1.75)^3+9(-1.75)^2-9(-1.75)+6	1.0781
-1.74	9(-1.74)^3+9(-1.74)^2-9(-1.74)+6	1.4962
-1.73	9(-1.73)^3+9(-1.73)^2-9(-1.73)+6	1.9066
-1.72	9(-1.72)^3+9(-1.72)^2-9(-1.72)+6	2.3096
-1.71	9(-1.71)^3+9(-1.71)^2-9(-1.71)+6	2.705
-1.70	9(-1.7)^3+9(-1.7)^2-9(-1.7)+6	3.093

Use the Intermediate Value Theorem.  Look for a sign change.  Looking down the table, there is a sign change between -1.78 and -1.77.  With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.