Problem:  Use the remainder theorem to find the remainder when f(x) is divided by 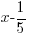.  Then use the factor theorem to determine whether 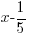is a factor of f(x).

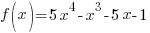
Solution:

The Remainder Theorem: Let f be a polynomial function.  If 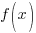is divided by 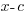, then the remainder is .

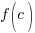The remainder theorem gives a way to find the remainder without performing the division.  The remainder when dividing by 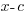is 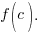  Calculate 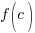to find the remainder where c is the zero of the factor .

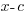For the example above, f(x) is divided by 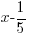.  The zero of the factor can be found by setting the factor equal to zero and solve.

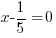
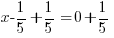
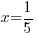
Use 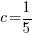and calculate .

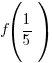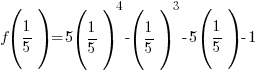
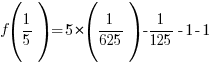
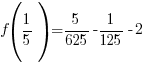
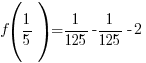
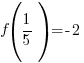
The remainder when f(x) is divided by 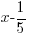is -2.

Factor Theorem: Let f be a polynomial function.  Then 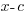is a factor of f(x) if and only if .

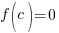This theorem gives of the result that if 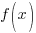is divided by 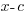and the remainder is zero, then 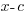is a factor of f.

For the example above, the remainder when f(x) is divided by 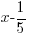is -2.  Since the remainder is not zero 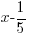is not a factor.