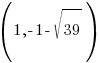Example: Find the center, foci, and vertices of the ellipse. Graph the equation.
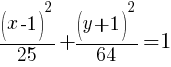
Solution:
Finding the center:
There are two standard orientations of ellipse’s, both of them have the center at (h,k).
Horizontal: 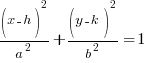
Vertical: 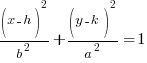
For this example the center of the ellipse is (1,-1)
Finding the orientation:
The larger denominator will indicate the orientation. Since our example has a larger denominator under the y variable the orientation is vertical. That means the ellipse is longer vertically.
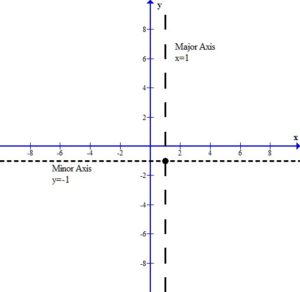
Finding the vertices: (Major Axis)
a is the distance between the center and the vertex along the major or longer axis. Since our larger denominator is 64 a is 8. I know this because the in the formula the larger denominator is 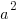 . If
. If 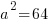 then
then 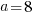 .
.
Since the ellipse is vertically oriented the vertices will be 8 units above and below the center.
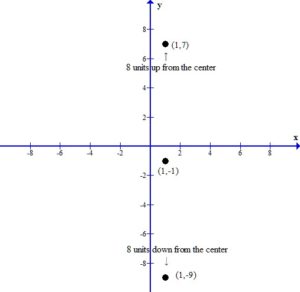
This puts the vertices at (1,7) and (1,-9).
Finding the vertices: (Minor Axis)
b is the distance between the center and the vertex along the minor or shorter axis. Since our smaller denominator is 25 b is 5. I know this because the in the formula the smaller denominator is 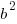 . If
. If 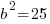 then
then 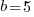 .
.
Since the ellipse is vertically oriented the vertices along the minor axis or shorter axis will be 5 units left and right of the center.
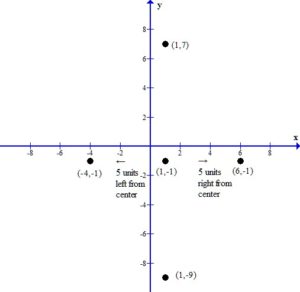
This puts the vertices at (-4,-1) and (6,-1).
Finding the foci:
c is the distance between the center and the focus. You can not find c from the equation. You must know that a, b, and c are related in a similar formula to Pythagorean theorem.
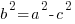
Fill in a and b, then you will be able to solve for c.
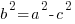
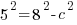
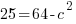
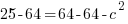
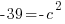
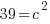
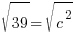
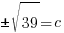
Since c is a distance we will use the positive solution. 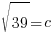 .
.
Since the ellipse is vertically oriented the foci will be 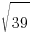 above and below the center.
above and below the center.
This puts the foci at 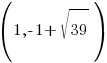 and
and