2.2 Circles, 2.3 Circles, Analyze

Writing an equation of a circle in standard form

Example:  Write the equation of a circle in standard form.

x^2+y^2+4x-8y+11=0

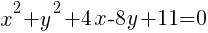
Start by grouping the x terms together, grouping the y terms together and moving the constant to the other side of the equation.

x^2+4x+y^2-8y=-11

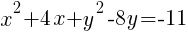
Use completing the square on the group of x terms and the group of y terms.

To find the number that completes the square for the x group, start with the coefficient of the x term, half it and square it.  The coefficient of the x term is 4

  (4/2)^2=4

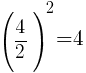
To find the number that completes the square for the y group, start with the coefficient of the y term, half it and square it.  The coefficient of the y term is -8

  (-8/2)^2=16

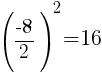
Add these numbers to the group of x terms and the group of y terms.  Be careful to maintain the balance of the equation by adding the numbers to both sides of the equation.

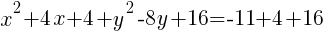
x^2+4x+4+y^2-8y+16=-11+4+16

(x^2+4x+4)+(y^2-8y+16)=-11+4+16

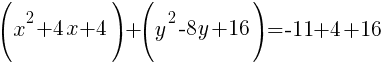
Now the group of x terms is a perfect square trinomial and will factor to be a binomial squared.  The group of y terms will do the same.

(x+2)(x+2)+(y-4)(y-4)=9

(x+2)^2+(y-4)^2=9

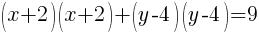
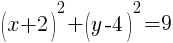
The equation of the circle is written in standard form where it is easy to recognize the center and radius of the circle.

The center is (-2,4) and the radius is 9.