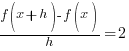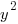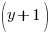Here is a handout with some of the significant definitions and properties related to rational functions.
Category Archives: MAC1140
Linear Modeling Applications
Maximize Enclosed Rectangular Area
Evaluating Inverse Functions with a graph
Domain and Range of Inverse Functions
Application of Systems of Linear Equations
Problem:
Benjamin & Associates, a real estate developer, recently built condominiums in McCall, Idaho. The condos were either two-bedroom units or three-bedroom units. If the total number of bedrooms in the entire complex is 498, how many two-bedroom units are there? How many three-bedroom units are there?
Solution:
Assign variables to the values we are looking for in the equation.
Let x be the number of two-bedroom units.
Let y be the number of three-bedroom units.
Create equations using the information given in the problem.
Since there are 199 condos built in the complex, the number of two-bedroom units plus the three bedroom units should equal the total units of 199.
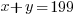
Since there are a total of 498 bedrooms in the complex, 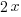 represents number of bedrooms coming from two-bedroom units, and
represents number of bedrooms coming from two-bedroom units, and 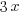 represents number of bedrooms coming from three-bedroom units, the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.
represents number of bedrooms coming from three-bedroom units, the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.
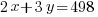
Solve the system of equations.
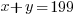
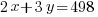
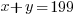 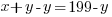 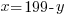 |
|
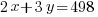 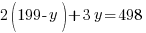 |
|
|
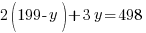 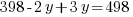 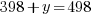 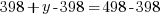 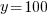 |
y represents the number of three-bedroom units. There are 100 three-bedroom units.
x represents the number of two-bedroom units. There are 199-100=99 two-bedroom units.
Polynomial Equation (Solve by factoring with the grouping method)
Example: Solve the polynomial equation
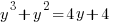
Solution: Solve the polynomial equation by factoring.
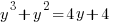 |
|
|
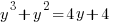 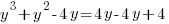 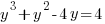 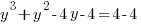 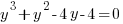 |
|
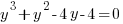 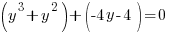 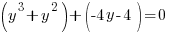 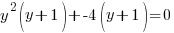 |
|
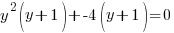 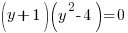 |
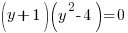 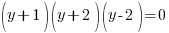 |
|
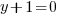 or or 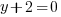 or or 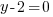 |
|
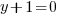 or or 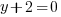 or or 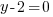 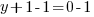 or or 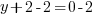 or or 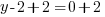 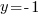 or or 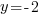 or or 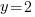 |
The solutions to the polynomial equation 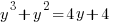 are
are 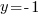 or
or 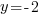 or
or 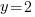 .
.
Solving Quadratic, Polynomial, and Rational Inequalities Graphically
Here is a worksheet to help you practice with polynomial and rational inequalities.
Solving Polynomial and Rational Inequalities Graphically
Here are the solutions to the worksheet above.
Solving Polynomial and Rational Inequalities Graphically Solutions updated
Difference Quotient: Linear Function
Example: Find the difference quotient for 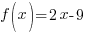
The Difference Quotient: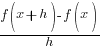
Solution:
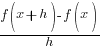 |
|
| Write the difference quotient for the given function | 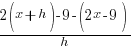 |
| Use the distributive property | 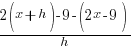 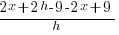 |
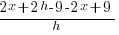 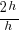 |
|
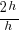 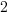 |
The difference quotient for the function 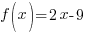 is
is