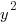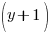Here is a handout with some of the significant definitions and properties related to rational functions.
Category Archives: MAC1105
Maximize Enclosed Rectangular Area
Evaluating Inverse Functions with a graph
Domain and Range of Inverse Functions
Application of Systems of Linear Equations
Problem:
Benjamin & Associates, a real estate developer, recently built condominiums in McCall, Idaho. The condos were either two-bedroom units or three-bedroom units. If the total number of bedrooms in the entire complex is 498, how many two-bedroom units are there? How many three-bedroom units are there?
Solution:
Assign variables to the values we are looking for in the equation.
Let x be the number of two-bedroom units.
Let y be the number of three-bedroom units.
Create equations using the information given in the problem.
Since there are 199 condos built in the complex, the number of two-bedroom units plus the three bedroom units should equal the total units of 199.
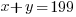
Since there are a total of 498 bedrooms in the complex, 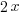 represents number of bedrooms coming from two-bedroom units, and
represents number of bedrooms coming from two-bedroom units, and 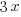 represents number of bedrooms coming from three-bedroom units, the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.
represents number of bedrooms coming from three-bedroom units, the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.
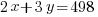
Solve the system of equations.
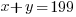
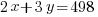
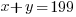 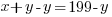 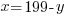 |
|
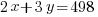 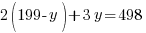 |
|
|
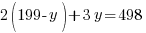 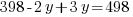 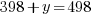 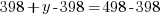 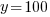 |
y represents the number of three-bedroom units. There are 100 three-bedroom units.
x represents the number of two-bedroom units. There are 199-100=99 two-bedroom units.
Polynomial Equation (Solve by factoring with the grouping method)
Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 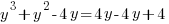 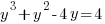 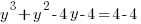 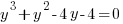 |
|
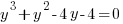 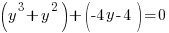 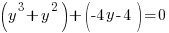 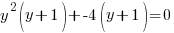 |
|
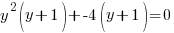 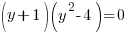 |
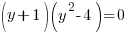 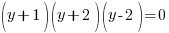 |
|
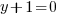 or or 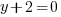 or or 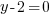 |
|
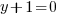 or or 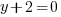 or or 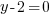 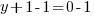 or or 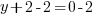 or or 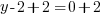 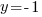 or or 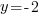 or or 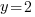 |
The solutions to the polynomial equation  are
are 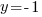 or
or 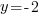 or
or 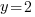 .
.
Solving a Quadratic Equation using the Quadratic Formula: Example 1 of 1
Example: Solve the quadratic equation with the quadratic formula.
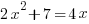
Solution:
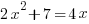 |
|
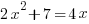 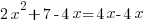 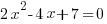 |
|
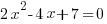 |
|
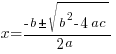 |
|
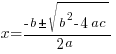 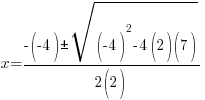 |
|
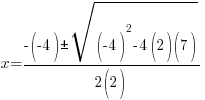 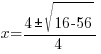 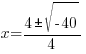 |
|
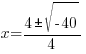 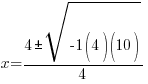 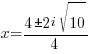 |
|
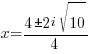 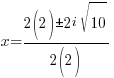 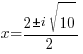 |
The solutions to the quadratic equation are 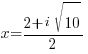 and
and 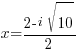 .
.
Solving Quadratic Equations by Factoring: Trinomial a=1
Example: Solve the quadratic equation by factoring.
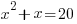
Solution:
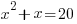 |
|
| Write the equation with all the terms on one side of the equation and zero on the other side of the equation. | 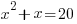 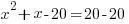 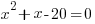 |
| Factor the expression on one side. | 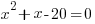 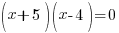 |
| Use the zero product property and set each factor equal to zero. | 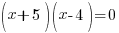 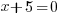 or or 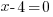 |
| Solve each equation. | 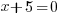 or or 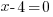 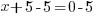 or or 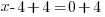 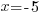 or or 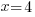 |
Check: 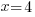
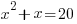
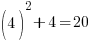
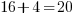
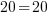
Since the value of 4 makes the equation true, 4 is a solution to the equation.
Check: 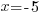
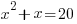
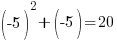
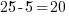
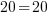
Since the value of -5 makes the equation true, -5 is a solution to the equation.
Solving a Quadratic Equation by Factoring: Difference of Squares
Example: Solve the quadratic equation by factoring.
 |
|
| The equation already has all of the terms on the same side and zero on the other side. |  |
| Factor the expression on one side. The expression for this equation is a difference of squares. |  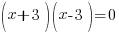 |
| Use the zero product property and set each factor equal to zero. | 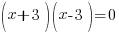 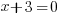 or or 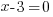 |
| Solve each equation. | 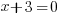 or or 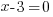 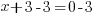 or or 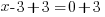 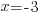 or or 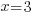 |
Solving a Quadratic Equation: The Square Root Method Example 1 of 1
Example: Solve the quadratic equation with completing the square.

 |
|
| Rewrite the quadratic equation so that the square and everything that the square applies to are on one side of the equation. This is called isolating the square. |  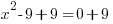 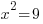 |
| Cancel out the square by square rooting both sides. | 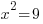 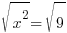 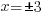 |
| The remaining equations are already solved. The solutions to the equation are 3 and -3. | 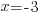 or or 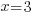 |