Graphing an Exponential Function (Base Function)
Solve a Linear Equation: Clearing Decimals
https://www.youtube.com/watch?v=AY8kS_BjCfE
Solving Linear Equations: Two Step Equations
Exponents: Simplify
Example: Rewrite the expression in the form 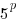 where p is an algebraic expression.
where p is an algebraic expression.
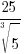
Solution:
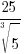 |
|
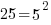 |
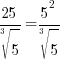 |
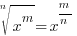 . For this example . For this example 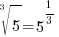 |
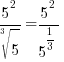 |
Quotient Rule for Exponents 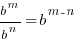 |
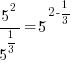 |
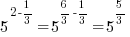 |
Finding Domain: Radical/Root Function (Even Root)
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
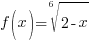
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 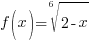 has a radical and the index is even. This function is a root function.
has a radical and the index is even. This function is a root function.
Find the Domain of a Root Function (Even Index)
Taking the even root of a negative number results in a complex or imaginary number. Since we are interested in real function values, we would like the expression inside the radical to be non-negative ( zero or positive) The root function is defined for any value of the variable where the expression under the radical is non-negative (zero or positive). Find these values by creating an inequality to solve. The inequality is the expression under the radical greater than or equal to zero.
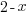 |
|
| Solve the inequality. This inequality is a linear inequality and can be solved by isolating the variable on one side. | 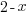 |
| Solve by isolating the variable. Start by subtracting 2 on both sides. | 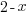 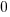 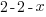 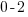 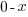 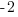 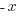 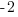 |
| Isolate the variable. Continue by dividing both sides by -1. Be sure to reverse the inequality symbol since you are dividing both sides by a negative. | 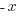 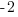 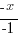 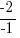 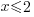 |
The function values where 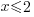 are defined for
are defined for 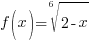 .
.
In set builder notation, the domain is ![]() .
.
In interval notation, the domain is (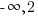 ]
]
Inequalities: Rational Inequalities
Application of Exponential Functions: Doubling Time
Example:
How long does it take for an investment to double if it is invested at 18% compounded continuously?
Solution:
Since this question involve continuous compound interest, we will use the associated formula.
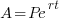
We are given that the interest rate is 18% or 0.18. This tells me that when r=0.18 Since we are looking for the doubling time, A will be 2 times P. I can write that in symbols A=2P.
Substitute these values into the continuous compound formula and solve for the interest rate.
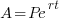 |
|
| Substitute the values of r and A into the formula | 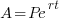 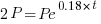 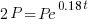 |
| Solve for t by dividing both sides by P and simplifying | 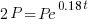 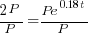 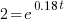 |
| Solve for t by taking the log of both sides. | 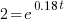 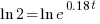 |
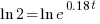 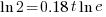 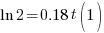 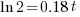 |
|
| Solve for t by dividing both sides by 0.18 and simplifying | 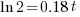 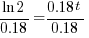 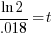 |
| Find the value in the calculator | 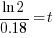 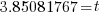 |
| Write the answer rounded to two decimal places | 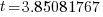 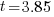 |
It will take 3.85 years to double your money when interest is compounded continuously at 18%.
If you need to write this in years and months, you will need to convert the 0.85 to months. Since there are 12 months in a year, multiply 0.85 by 12 to get 10.2. I will round to the nearest months to get 10.
It will take 3 years and 10 months to double your money when interest is compounded continuously at 18%.
Here is a video that is similar except that you are looking for the investment to triple.
Polynomial Function: Finding Zeros and Write in Factored Form
Problem: Use the rational zeros theorem to find all real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
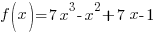
Since f is a polynomial function with integer coefficients use the rational zeros theorem to find the possible zeros.
The factors of the constant term, 1 are p.
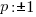
The factors of the leading coefficient, 7 are q.
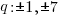
The possible rational zeros can be found by working out all of the possible combinations of p/q.
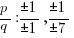
Simplifying these combinations give 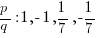
To test if any of these potential zeros are actual zeros, evaluate the function at these values.
| x | f(x) | f(x) |
|---|---|---|
| -1 | 7(-1)^3-(-1)^2+7(-1)-1 | -16 |
| -1/7 | 7(-1/7)^3-(-1/7)^2+7(-1/7)-1 | -2.041 |
| 1/7 | 7(1/7)^3-(1/7)^2+7(1/7)-1 | 0 |
| 1 | 7(1)^3-(1)^2+7(1)-1 | 12 |
This can be completed quickly using the ask feature in your calculator.




Since f(1/7) is zero, 1/7 is a zero of the function. Since the function has a zero of 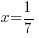 then the function has a factor of
then the function has a factor of 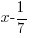
Use long division or synthetic division to to reduce the polynomial.
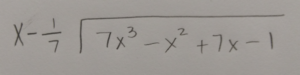 |
|
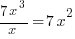 |
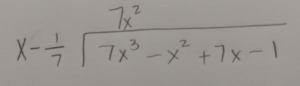 |
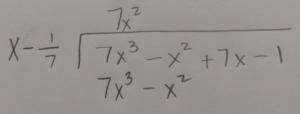 |
|
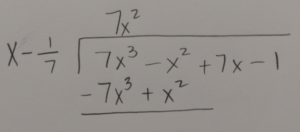 |
|
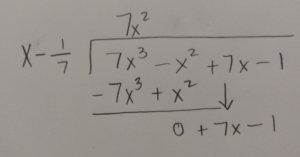 |
|
 |
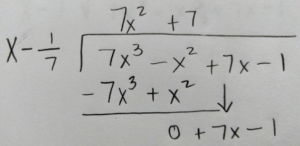 |
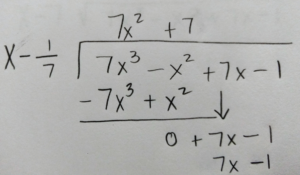 |
|
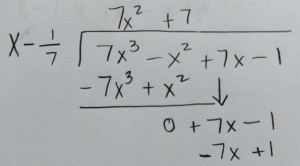 |
|
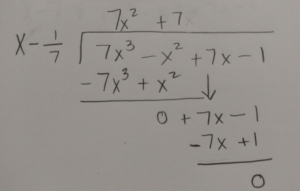 |
Write the function in factored form using the results of the long division.
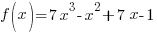
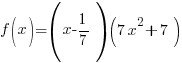
Factor completely.
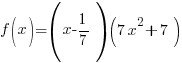
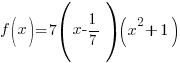
Intermediate Value Theorem
Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval. Approximate the zero to two decimal places.
![f(x)=9x^3+9x^2-9x+6; [-2,-1] f(x)=9x^3+9x^2-9x+6; [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_8c3d8866a3f884f4b90f75e40f6be143.png)
Solution:
To determine if there is a zero in the interval use the Intermediate Value theorem. To use the Intermediate Value Theorem, the function must be continuous on the interval ![[-2,-1] [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ffd21cf987ccbaa47dd393edf5d2bd04.png) . The function
. The function 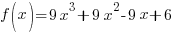 is a polynomial function and polynomial functions are defined and continuous for all real numbers.
is a polynomial function and polynomial functions are defined and continuous for all real numbers.
Evaluate the function at the endpoints and if there is a sign change. If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval. To evaluate the function at the endpoints, calculate 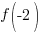 and
and 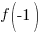 .
.
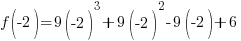
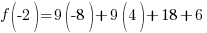
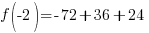
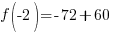
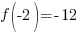
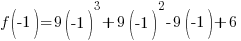
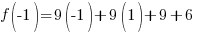
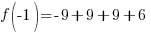
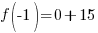
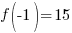
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.
We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.
| x | f(x) | f(x) |
|---|---|---|
| -2.0 | 9(-2)^3+9(-2)^2-9(-2)+6 | -12 |
| -1.9 | ||
| -1.8 | ||
| -1.7 | ||
| -1.6 | ||
| -1.5 | ||
| -1.4 | ||
| -1.3 | ||
| -1.2 | ||
| -1.1 | ||
| -1.0 | 9(-1)^3+9(-1)^2-9(-1)+6 | 15 |
Fill the table. There are functions in your calculator that make this easier.



| x | f(x) | f(x) |
|---|---|---|
| -2.0 | 9(-2)^3+9(-2)^2-9(-2)+6 | -12 |
| -1.9 | 9(-1.9)^3+9(-1.9)^2-9(-1.9)+6 | -6.141 |
| -1.8 | 9(-1.8)^3+9(-1.8)^2-9(-1.8)+6 | -1.128 |
| -1.7 | 9(-1.7)^3+9(-1.7)^2-9(-1.7)+6 | 3.093 |
| -1.6 | 9(-1.6)^3+9(-1.6)^2-9(-1.6)+6 | 6.576 |
| -1.5 | 9(-1.5)^3+9(-1.5)^2-9(-1.5)+6 | 9.375 |
| -1.4 | 9(-1.4)^3+9(-1.4)^2-9(-1.4)+6 | 11.544 |
| -1.3 | 9(-1.3)^3+9(-1.3)^2-9(-1.3)+6 | 13.137 |
| -1.2 | 9(-1.2)^3+9(-1.2)^2-9(-1.2)+6 | 14.208 |
| -1.1 | 9(-1.1)^3+9(-1.1)^2-9(-1.1)+6 | 14.811 |
| -1.0 | 9(-1)^3+9(-1)^2-9(-1)+6 | 15 |
Use the Intermediate Value Theorem again. Look for a sign change. Looking down the table, there is a sign change between -1.8 and -1.7. With this information we now know the zero is between these two values.
Repeat this process again with two decimal places between -1.8 and -1.7.


| x | f(x) | f(x) |
|---|---|---|
| -1.80 | 9(-1.8)^3+9(-1.8)^2-9(-1.8)+6 | -1.128 |
| -1.79 | 9(-1.79)^3+9(-1.79)^2-9(-1.79)+6 | -.6712 |
| -1.78 | 9(-1.78)^3+9(-1.78)^2-9(-1.78)+6 | -.2222 |
| -1.77 | 9(-1.77)^3+9(-1.77)^2-9(-1.77)+6 | .219 |
| -1.76 | 9(-1.76)^3+9(-1.76)^2-9(-1.76)+6 | .65242 |
| -1.75 | 9(-1.75)^3+9(-1.75)^2-9(-1.75)+6 | 1.0781 |
| -1.74 | 9(-1.74)^3+9(-1.74)^2-9(-1.74)+6 | 1.4962 |
| -1.73 | 9(-1.73)^3+9(-1.73)^2-9(-1.73)+6 | 1.9066 |
| -1.72 | 9(-1.72)^3+9(-1.72)^2-9(-1.72)+6 | 2.3096 |
| -1.71 | 9(-1.71)^3+9(-1.71)^2-9(-1.71)+6 | 2.705 |
| -1.70 | 9(-1.7)^3+9(-1.7)^2-9(-1.7)+6 | 3.093 |
Use the Intermediate Value Theorem. Look for a sign change. Looking down the table, there is a sign change between -1.78 and -1.77. With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.
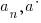 are from the real numbers.
are from the real numbers.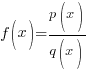
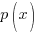 and
and 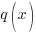 are polynomial functions and
are polynomial functions and