Example: Find the partial fraction decomposition for the rational expression.
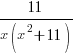
Solution:
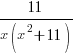 |
|
| Factor the denominator completely | 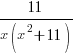 |
| Write the expression with each factor as a separate fraction. | 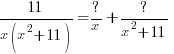 |
| Decide what type of expression to put in the numerator
x is linear so we put a constant in the numerator
|
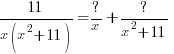 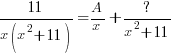 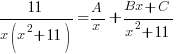 |
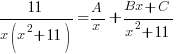 |
|
Multiply both sides of the equation by the common denominator 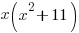 and simplify by canceling out common factors and simplify by canceling out common factors |
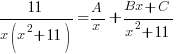 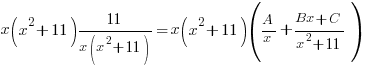 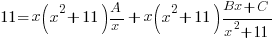 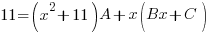 |
| Use the distributive property and collect the like terms with the x’s | 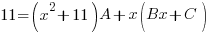 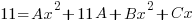 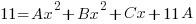 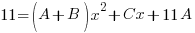 |
| Equate coefficients to create a system of equations to solve | 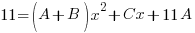 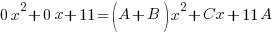 |
| On the left 11 is the constant term. There is no linear term so the coefficient is zero and there is no quadratic term so the coefficient is zero.
On the right the constant (no x’s) is 11A, the linear coefficient is C and the quadratic coefficient is A+B. |
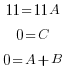 |
Now solve the system of equations.
The first equation is 11=11A. Since it only has one variable, I can solve for A by hand.
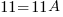
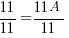
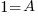
The second equation is 0=C . It is already solved.
The third equation is 0=A+B. Since I know A=1, I can substitute and solve for B.
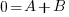
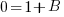
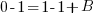
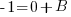
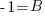
Using the original set up of 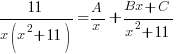 , substitute the values of A, B, and C.
, substitute the values of A, B, and C.
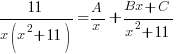
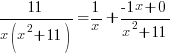
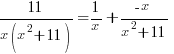
The partial fraction decomposition of 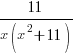 is
is 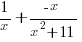
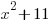 is a quadratic so we put a linear expression in the numerator
is a quadratic so we put a linear expression in the numerator