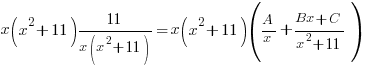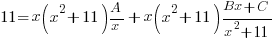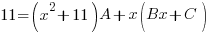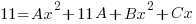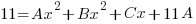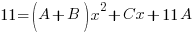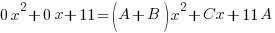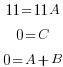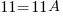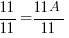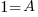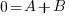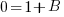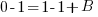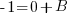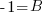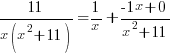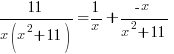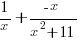Category Archives: Sullivan Chapter 8

7.1 Systems of Linear Equations in Two Variables, 8.1 Systems of Linear Equations: Substitution and Elimination

Application of Systems of Linear Equations

Problem:

Benjamin & Associates, a real estate developer, recently built condominiums in McCall, Idaho.  The condos were either two-bedroom units or three-bedroom units.  If the total number of bedrooms in the entire complex is 498, how many two-bedroom units are there?  How many three-bedroom units are there?

Solution:

Assign variables to the values we are looking for in the equation.

Let x be the number of two-bedroom units.
Let y be the number of three-bedroom units.

Create equations using the information given in the problem.

Since there are 199 condos built in the complex, the number of two-bedroom units plus the three bedroom units should equal the total units of 199.

x+y=199

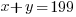
Since there are a total of 498 bedrooms in the complex, 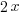2x represents number of bedrooms coming from two-bedroom units, and 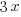3x represents number of bedrooms coming from three-bedroom units,  the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.

2x+3y=498

 

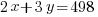
Solve the system of equations.

x+y=199
2x+3y=498

 

Solve one equation for one of the variables.  Choose to solve for x in the first equation since it doesn’t have a coefficient and fractions can be avoided that way.
x+y=199
x+y-y=199-y
x=199-y
Substitute the expression into the other equation.
2x+3y=498
2(199-y)+3y=498
Solve for the other variable. 

  • Use the distributive property to remove parenthesis.
  • Combine like terms
  • Isolate the variable on one side of the equation
2(199-y)+3y=498
398-2y+3y=498
398+y=498
398+y-398=498-398
y=100

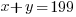
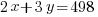
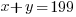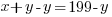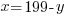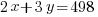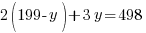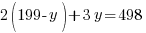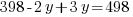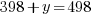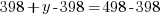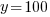y represents the number of three-bedroom units.  There are 100 three-bedroom units.

x represents the number of two-bedroom units.  There are 199-100=99 two-bedroom units.

8.5 Partial Fraction Decomposition

Partial Fraction Decomposition

Example:  Find the partial fraction decomposition for the rational expression.

11/{x(x^2+11)}

Solution:

The rational expression
 11/{x(x^2+11)}
Factor the denominator completely
11/{x(x^2+11)}
Write the expression with each factor as a separate fraction.
11/{x(x^2+11)}=?/x+?/{x^2+11}
Decide what type of expression to put in the numerator

x is linear so we put a constant in the numerator

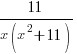
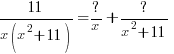
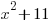x^2+11 is a quadratic so we put a linear expression in the numerator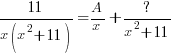
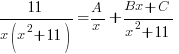
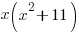11/{x(x^2+11)}=?/x+?/{x^2+11}
11/{x(x^2+11)}=A/x+?/{x^2+11}
11/{x(x^2+11)}=A/x+{Bx+C}/{x^2+11}
Now that the set up is done we need to solve for the unknowns A, B and C
11/{x(x^2+11)}=A/x+{Bx+C}/{x^2+11}
Multiply both sides of the equation by the common denominator {x(x^2+11)} and simplify by canceling out common factors
11/{x(x^2+11)}=A/x+{Bx+C}/{x^2+11}
{x(x^2+11)}11/{x(x^2+11)}={x(x^2+11)}(A/x+{Bx+C}/{x^2+11})
11={x(x^2+11)}{A/x}+{x(x^2+11)}{Bx+C}/{x^2+11}
11={(x^2+11)}{A}+x(Bx+C)
Use the distributive property and collect the like terms with the x’s
11={(x^2+11)}{A}+x(Bx+C)
11=Ax^2+11A+Bx^2+Cx
11=Ax^2+Bx^2+Cx+11A
11=(A+B)x^2+Cx+11A
Equate coefficients to create a system of equations to solve
11=(A+B)x^2+Cx+11A
0x^2+0x+11=(A+B)x^2+Cx+11A
On the left 11 is the constant term.  There is no linear term so the coefficient is zero and there is no quadratic term so the coefficient is zero.

On the right the constant (no x’s) is 11A, the linear coefficient is C and the quadratic coefficient is A+B.
System of equations from equating the coefficients
matrix{3}{1}{{11=11A} {0=C} {0=A+B}}

Now solve the system of equations.

The first equation is  11=11A.  Since it only has one variable, I can solve for A by hand.

11=11A
11/11={11A}/11
1=A

The second equation is 0=C .  It is already solved.

The third equation is 0=A+B.  Since I know A=1, I can substitute and solve for B.

0=A+B
0=1+B
0-1=1-1+B
-1=0+B
-1=B

Using the original set up of 11/{x(x^2+11)}=A/x+{Bx+C}/{x^2+11}, substitute the values of A, B, and C.

11/{x(x^2+11)}=A/x+{Bx+C}/{x^2+11}
11/{x(x^2+11)}=1/x+{-1x+0}/{x^2+11}
11/{x(x^2+11)}=1/x+{-x}/{x^2+11}

The partial fraction decomposition of 11/{x(x^2+11)} is 1/x+{-x}/{x^2+11}