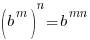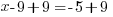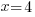Category Archives: 6.6 Logarithmic and Exponential Equations
Logarithmic Equations: Convert to Exponential
https://www.youtube.com/watch?v=G_kHwdrxyeU
Logarithmic Equations: One-to-One Property or Property of Equality
Exponential Equations: Same Base
Solve an Exponential Equation: Relating the Bases
Problem: Solve the exponential equation.
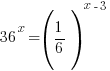
Solution:
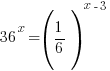 |
|
The bases of the exponents on each side of the equation can be made the same. 36 can be written as 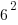 and and 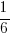 can be written as can be written as 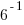 |
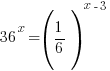 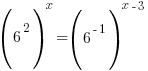 |
|
Use the power rule for exponents to multiply the exponents. |
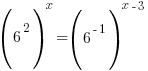 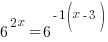 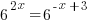 |
| Exponential functions are one-to-one thus giving us the property that if the bases are the same the exponents are equal. If 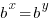 then then 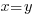 |
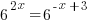 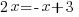 |
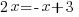 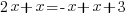 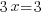
|
|
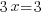 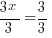  |
|
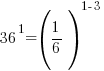 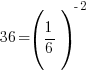 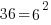 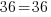 |
The solution to the equation 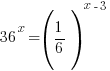 is
is  .
.
Here is a video example of a similar type of problem.
Solve an exponential equation: Take the log of both sides
Example:
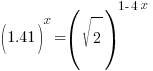
Solution:
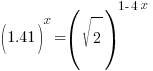 |
|
| Since the bases cannot be easily written the same use the method of taking the log of both sides | 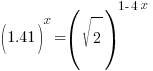 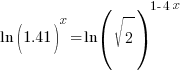 |
| Use the power rule for logarithms | 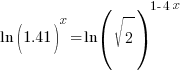 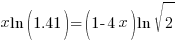 |
| Use the distributive law | 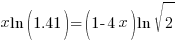 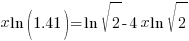 |
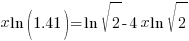 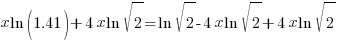 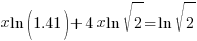 |
|
| Factor the common x | 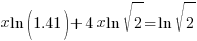 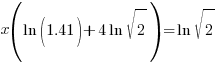 |
| Solve for x by dividing both sides by the factor in the parenthesis and simplify | 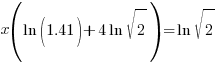 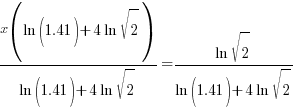 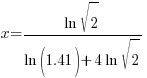 |
| The solution | 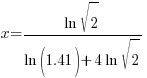 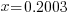 |
When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator. Here is an example of how you might enter it.
(ln (sqrt{2}))/(ln(1.41)+4 ln(sqrt{2}))
Here is a youtube video with a similar example.
Solve the Logarithmic Equation by the one to one property
Example:
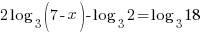
Solution:
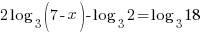 |
|
| Use the power rule and the quotient rule to condense to a single logarithm | 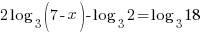 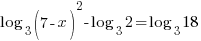 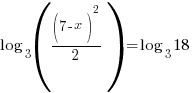 |
| Since both sides of the equation have the same log base the expressions inside the logarithms must be equal | 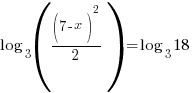 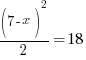 |
| Clear the denominator by multiplying by 2 on both sides and simplifying | 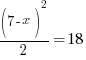 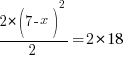 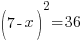 |
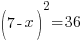 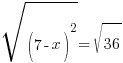 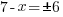 |
|
| Get x by itself by subtracting 7 on both sides | 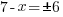 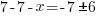 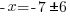 |
| Get x by itself by dividing both sides by negative 1 | 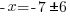 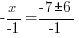 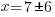 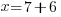 or or 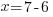 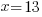 or or  |
| Check x=13 | 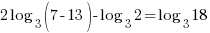 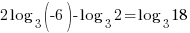 |
| Check x=1 | 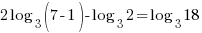 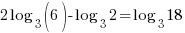 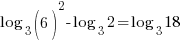 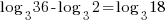 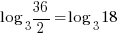 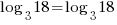 |
The solution to the equation is x=1.
Here is a youtube video that is similar.
Solve an Exponential Equation: Take the log of both sides
Problem: Solve the exponential equation.
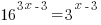
Solution:
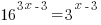 |
|
| Since the bases cannot be easily written the same, use the method of taking the log of both sides | 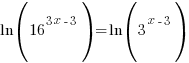 |
| Use the power rule for logarithms. | 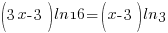 |
| Use the distributive property. | 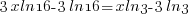 |
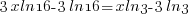 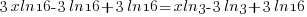 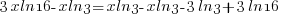 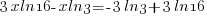 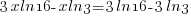 |
|
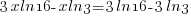 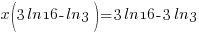 |
|
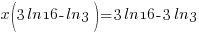 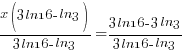 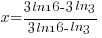 |
|
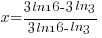 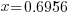 |
When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator. Here is an example of how you might enter it.
(3ln(16)-3ln(3))/(3ln(16)-ln(3))
Solving an Exponential Equation: Relating the Bases
Example: Solve the exponential equation.
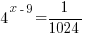
Solution:
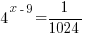 |
|
| Try to write both sides of the equation with the same base. Try 4 since there is a base of 4 on the left | 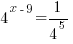 |
| Using a property of negative exponents move the base to the numerator | 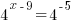 |
| Now that that the bases are the same the exponents must be equal | 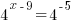
|
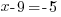
|
The solution the the exponential equation is 4.
Here is a youtube video with a similar example.