Problem: Use the properties of logarithms to rewrite the expression as a single logarithm. Whenever possible, evaluate logarithmic expressions.
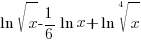
Soluton:
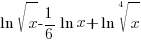 |
|
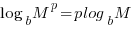 |
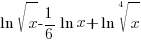 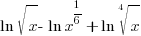 |
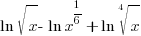 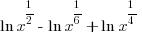 |
|
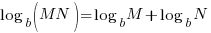 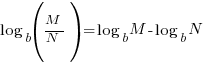 |
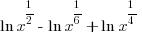 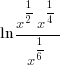 |
| Since these base of the exponential expressions are the same, combine using the power and quotient rules for exponent. Product Rule for Exponents: 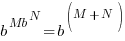 Quotient Rule for Exponents: 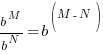 |
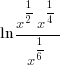 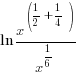 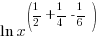 |
| Find a common denominator to combine the fractions. | 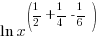 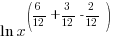 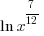 |
Here is a video with a similar example worked out.