Category Archives: Sullivan Chapter 5
Inequalities: Rational Inequalities
Polynomial Function: Finding Zeros and Write in Factored Form
Problem: Use the rational zeros theorem to find all real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
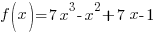
Since f is a polynomial function with integer coefficients use the rational zeros theorem to find the possible zeros.
The factors of the constant term, 1 are p.
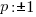
The factors of the leading coefficient, 7 are q.
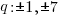
The possible rational zeros can be found by working out all of the possible combinations of p/q.
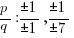
Simplifying these combinations give 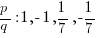
To test if any of these potential zeros are actual zeros, evaluate the function at these values.
This can be completed quickly using the ask feature in your calculator.




Since f(1/7) is zero, 1/7 is a zero of the function. Since the function has a zero of 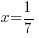 then the function has a factor of
then the function has a factor of 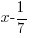
Use long division or synthetic division to to reduce the polynomial.
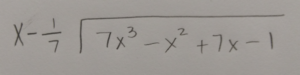 |
|
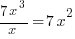 |
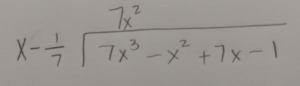 |
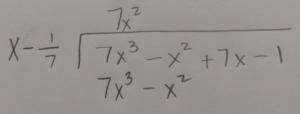 |
|
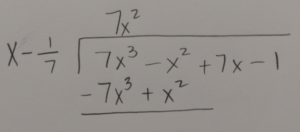 |
|
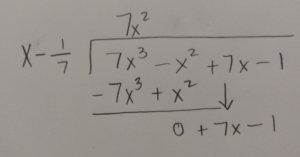 |
|
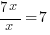 |
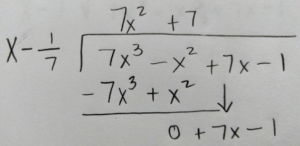 |
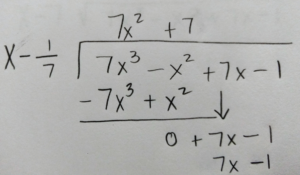 |
|
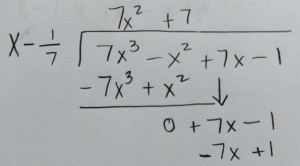 |
|
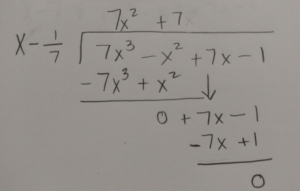 |
Write the function in factored form using the results of the long division.
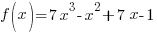
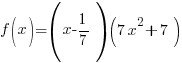
Factor completely.
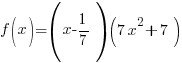
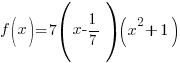
Intermediate Value Theorem
Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval. Approximate the zero to two decimal places.
![f(x)=9x^3+9x^2-9x+6; [-2,-1] f(x)=9x^3+9x^2-9x+6; [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_8c3d8866a3f884f4b90f75e40f6be143.png)
Solution:
To determine if there is a zero in the interval use the Intermediate Value theorem. To use the Intermediate Value Theorem, the function must be continuous on the interval ![[-2,-1] [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ffd21cf987ccbaa47dd393edf5d2bd04.png) . The function
. The function 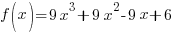 is a polynomial function and polynomial functions are defined and continuous for all real numbers.
is a polynomial function and polynomial functions are defined and continuous for all real numbers.
Evaluate the function at the endpoints and if there is a sign change. If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval. To evaluate the function at the endpoints, calculate 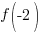 and
and 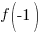 .
.
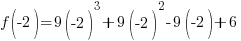
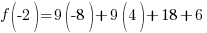
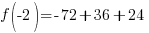
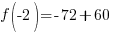
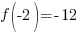
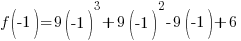
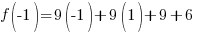
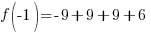
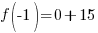
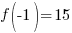
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.
We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.
Fill the table. There are functions in your calculator that make this easier.



Use the Intermediate Value Theorem again. Look for a sign change. Looking down the table, there is a sign change between -1.8 and -1.7. With this information we now know the zero is between these two values.
Repeat this process again with two decimal places between -1.8 and -1.7.


Use the Intermediate Value Theorem. Look for a sign change. Looking down the table, there is a sign change between -1.78 and -1.77. With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.
Remainder Theorem and Factor Theorem
Problem: Use the remainder theorem to find the remainder when f(x) is divided by 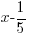 . Then use the factor theorem to determine whether
. Then use the factor theorem to determine whether 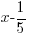 is a factor of f(x).
is a factor of f(x).
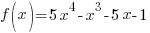
Solution:
The Remainder Theorem: Let f be a polynomial function. If 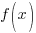 is divided by
is divided by 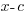 , then the remainder is
, then the remainder is 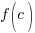 .
.
The remainder theorem gives a way to find the remainder without performing the division. The remainder when dividing by 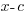 is
is 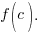 Calculate
Calculate 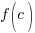 to find the remainder where c is the zero of the factor
to find the remainder where c is the zero of the factor 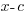 .
.
For the example above, f(x) is divided by 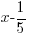 . The zero of the factor can be found by setting the factor equal to zero and solve.
. The zero of the factor can be found by setting the factor equal to zero and solve.
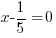
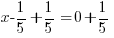
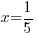
Use 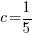 and calculate
and calculate 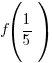 .
.
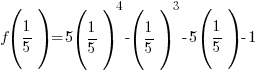
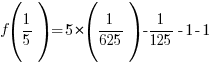
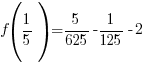
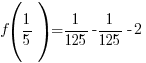
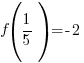
The remainder when f(x) is divided by 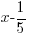 is -2.
is -2.
Factor Theorem: Let f be a polynomial function. Then 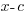 is a factor of f(x) if and only if
is a factor of f(x) if and only if 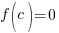 .
.
This theorem gives of the result that if 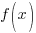 is divided by
is divided by 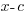 and the remainder is zero, then
and the remainder is zero, then 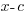 is a factor of f.
is a factor of f.
For the example above, the remainder when f(x) is divided by 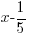 is -2. Since the remainder is not zero
is -2. Since the remainder is not zero 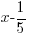 is not a factor.
is not a factor.
Rational Function: Sketch the graph of the rational function
Problem:
Sketch the graph of the rational function using algebra techniques.
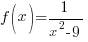
Solution:
To start sketching the graph, gather the following information about the graph.
Domain, vertical asymptotes, holes/removable discontinuities, horizontal asymptotes, oblique/slant asymptotes, points where the graph crosses the horizontal asymptotes, x-intercepts, and y-intercepts.
Find the Domain of a Rational Function
Division by zero is undefined. Having a zero as the denominator is equivalent to division by zero thus is also undefined. The rational function is undefined for any value of the variable that gives a zero denominator. Find these values by creating an equation to solve. The equation is the expression in the denominator equal to zero.
 |
|
| Solve the equation. This equation is a quadratic equation and can be solved by factoring, the square root method, completing the square or the quadratic formula. |  |
| Solve by the square root method. Start by isolating the square. |  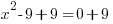 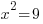 |
| Cancel out the square by square rooting both sides. | 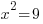 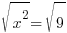 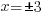 |
| The solutions to the equation are 3 and -3. | 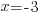 or or 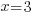 |
The values 3 and -3 give a zero value in the denominator and must be excluded from the domain.
In set builder notation, the domain is 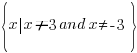
In interval notation, the domain is 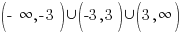
Find Vertical Asymptotes and Holes/Removable Discontinuities
A vertical asymptote occurs when there is a non-zero in the numerator and a zero in the denominator. To find the location of any vertical asymptotes, find the values where the denominator is zero but only after reducing the fraction so that we can guarantee that there is a non-zero in the numerator.
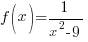 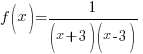 |
|
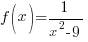 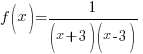 |
|
 |
|
| Solve the equation. This equation is a quadratic equation and can be solved by factoring, the square root method, completing the square or the quadratic formula. |  |
| Solve by factoring. Factor the expression on one side. |  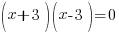 |
| Use the zero product property and set each factor equal to zero. | 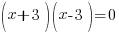 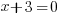 or or 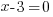 |
| Solve each equation. | 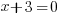 or or 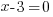 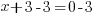 or or 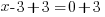 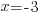 or or 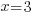 |
The rational function has vertical asymptotes at x=-3 and x=3. That means that y approaches 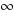 or
or 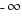 as x approaches the values of 3 and -3. Knowing this will guide us when sketching the graph.
as x approaches the values of 3 and -3. Knowing this will guide us when sketching the graph.
Determine if the graph has any holes/removable discontinuities. In this example, since the rational function was in lowest terms there is no hole/removable discontinuity.
Find Horizontal Asymptotes and Oblique/Slant Asymptotes
Find the horizontal asymptotes using a set of rules based on the degree of the numerator and the degree of the denominator.
Horizontal Asymptote and Oblique/Slant Cases
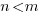 |
|
Case 2: The degree of the numerator is equal to the degree of the denominator.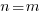 |
The horizontal asymptote is y= the ratio of the leading coefficients. There is no oblique/slant asymptote. |
Case 3: The degree of the numerator is one more than the degree of the denominator.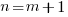 |
There is no horizontal asymptote. There is an oblique/slant asymptote. Find it using long division. |
| Case 4: The degree of the numerator is two or more than the degree of the denominator. |
There is no horizontal asymptote and there is no oblique/slant asymptote. |
For this example, the numerator is 1 and the degree of the numerator is 0. The denominator is 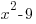 and the degree of the numerator is 2. Since the degree of the numerator is less than the degree of the denominator (case 1) the horizontal asymptote is y=0. That means that y approaches 0 as x approaches
and the degree of the numerator is 2. Since the degree of the numerator is less than the degree of the denominator (case 1) the horizontal asymptote is y=0. That means that y approaches 0 as x approaches 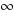 or
or 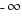 . Knowing this will guide us when sketching the graph.
. Knowing this will guide us when sketching the graph.
Find any Points that Cross the Horizontal or Oblique Asymptote
The horizontal and oblique asymptotes describe the graph as x approaches 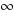 or
or 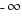 , usually called the end behavior. The graph will approach the asymptote but not reach the asymptote at the ends of the graph. However, the graph can cross the horizontal or oblique asymptote in the middle section of the graph. To find were the graph crosses the horizontal or oblique asymptote, set the value of the asymptote equal to the function.
, usually called the end behavior. The graph will approach the asymptote but not reach the asymptote at the ends of the graph. However, the graph can cross the horizontal or oblique asymptote in the middle section of the graph. To find were the graph crosses the horizontal or oblique asymptote, set the value of the asymptote equal to the function.
For this example, set the horizontal asymptote (y=0) equal to the function 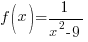 .
.
Horizontal Asymptote = Function
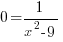
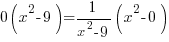
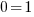
Since there is no solution to this equation, there are no points where the graph crosses the horizontal asymptote.
Find the Intercepts of the Rational Function
To find a y-intecept let x=0.
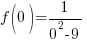
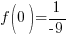
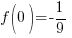
The y-intercept is 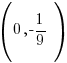
To find the x-intercept let y=0 or f(x)=0. Exclude solutions that were found to be undefined for the function when the domain was found.
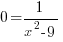
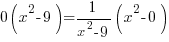
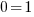
Since this equation has no solution. There is no x-intercept.
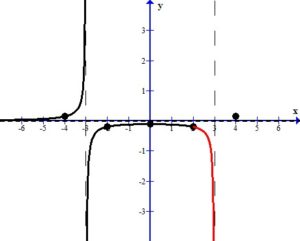
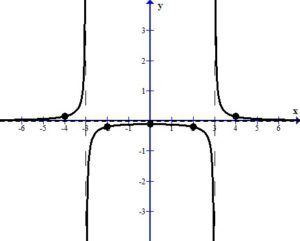
Sketch the Graph
Draw the asymptotes as dashed lines. These will be used as guides to draw the graph. For this example, the vertical asymptotes were at x=-3 and x=3 and the horizontal asymptote was at y=0.
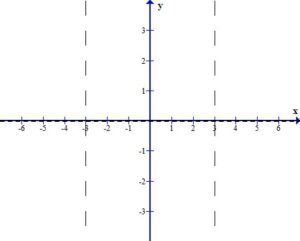
Plot the intercepts, holes or places where the graph crosses an asymptote. For this example, the only value is the y-intercept.
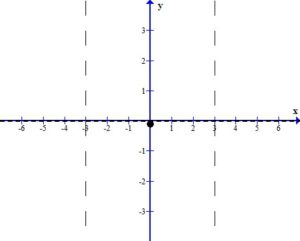
More points are needed to sketch the graph. Choose points in every section of the graph, using the vertical asymptotes to divide the sections up.
For example, choose x=-4 to represent the left section. The middle section needs a few extra points since it is surrounded by asymptotes. Choose x=-2 and x=2 to represent the middle section. Choose x=4 to represent the right section.
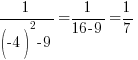 |
|
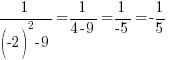 |
|
| 2 | 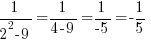 |
| 4 | 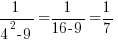 |
Plot the points on the graph.
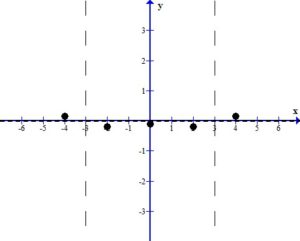
Use the definition of the asymptotes to draw the graph near each point.
In the left section, consider the graph as x approaches 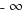 (
(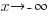 ).
).
Since the graph has a horizontal asymptote at y=0, 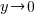 as
as 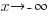 . As you draw the graph to the left of -4, approach the horizontal asymptote.
. As you draw the graph to the left of -4, approach the horizontal asymptote.
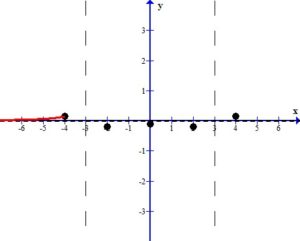
In the left section, consider the graph as x approaches -3 from the left (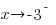 .)
.)
Since the graph has a vertical asymptote at x=-3, 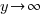 or
or 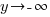 as
as 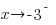 . Since the point in the left section lies above the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote,
. Since the point in the left section lies above the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote, 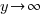 . As you draw the graph to the right of -4 approach the vertical asymptote going towards positive infinity.
. As you draw the graph to the right of -4 approach the vertical asymptote going towards positive infinity.
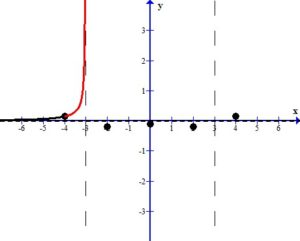
In the middle section, consider the graph as x approaches -3 from the right, (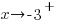 .)
.)
Since the graph has a vertical asymptote at x=-3, 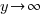 or
or 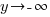 as
as 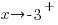 . Since the point near -3 in the middle section lies below the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote,
. Since the point near -3 in the middle section lies below the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote, 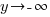 . As you draw the graph to the left of -2, approach the vertical asymptote going towards negative infinity.
. As you draw the graph to the left of -2, approach the vertical asymptote going towards negative infinity.
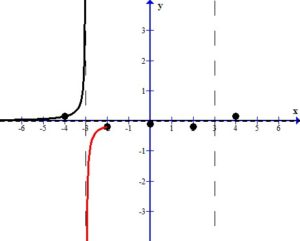
In the middle section, the three points can be connected to each other since there are no undefined values between them.
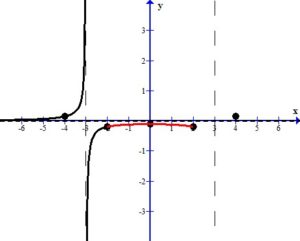
In the middle section, consider the graph as x approaches 3 from the left, (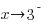 .)
.)
Since the graph has a vertical asymptote at x=3, 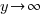 or
or 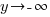 as
as 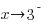 . Since the point near 3 in the middle section lies below the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote,
. Since the point near 3 in the middle section lies below the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote, 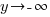 . As you draw the graph to the right of 2, approach the vertical asymptote going towards negative infinity.
. As you draw the graph to the right of 2, approach the vertical asymptote going towards negative infinity.
In the right section, consider the graph as x approaches 3 from the right (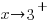 .)
.)
Since the graph has a vertical asymptote at x=3, 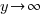 or
or 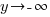 as
as 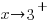 . Since the point in the right section lies above the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote,
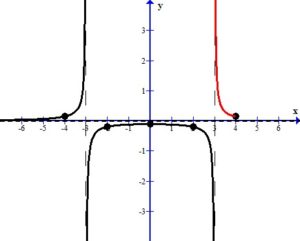
. Since the point in the right section lies above the horizontal asymptote and it was determined that the graph does not cross the horizontal asymptote, 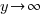 . As you draw the graph to the right of 4 approach the vertical asymptote going towards positive infinity.
. As you draw the graph to the right of 4 approach the vertical asymptote going towards positive infinity.
In the right section, consider the graph as x approaches 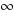 (
(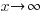 ).
).
Since the graph has a horizontal asymptote at y=0, 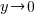 as
as 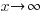 . As you draw the graph to the right of 4, approach the horizontal asymptote.
. As you draw the graph to the right of 4, approach the horizontal asymptote.
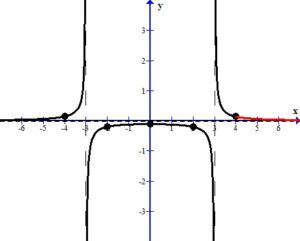
The sketch of the rational function 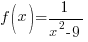 is below.
is below.
Here are some video examples that might help.
Form a Polynomial given the Degree and Zeros
Example: Form a polynomial f(x) with real coefficients having the given degree and zeros.
Degree 4; Zeros -2-3i; 5 multiplicity 2
Solution:
By the Fundamental Theorem of Algebra, since the degree of the polynomial is 4 the polynomial has 4 zeros if you count multiplicity.
There are three given zeros of -2-3i, 5, 5.
The remaining zero can be found using the Conjugate Pairs Theorem. f(x) is a polynomial with real coefficients. Since -2-3i is a complex zero of f(x) the conjugate pair of -2+3i is also a zero of f(x).
Now that all the zeros of f(x) are known the polynomial can be formed with the factors that are associated with each zero.
Since f(x) has a zero of 5, f(x) has a factor of x-5
Since f(x) has a second zero of 5, f(x) has a second factor of x-5
Since f(x) has a factor of -2-3i, f(x) has a factor of x-(-2-3i)
Since f(x) has a factor of -2+3i, f(x) has a factor of x-(-2+3i)
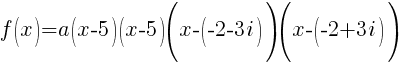 |
|
|
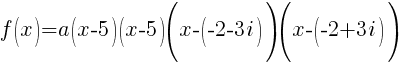 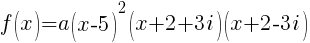 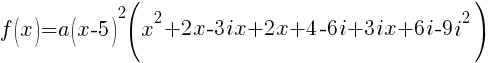 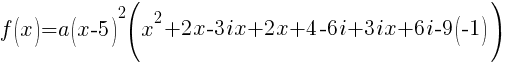 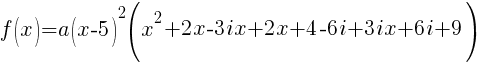 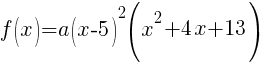 |
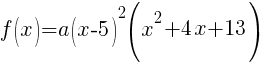 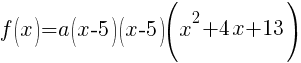 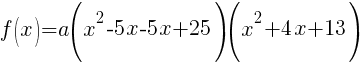 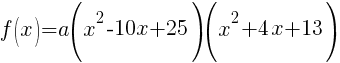 |
|
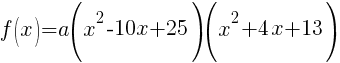 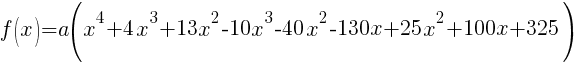 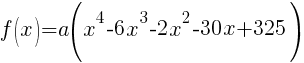 |
The polynomial with degree 4 and zeros of -2-3i and 5 wiht multiplicity 2 is 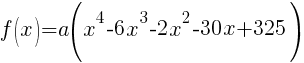
Finding Horizontal and Oblique (Slant) Asymptotes
Finding Vertical Asymptotes and Holes (Removable Discontinuity)
Finding Domain: Rational Function
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
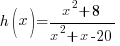
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 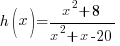 has a variable in the denominator and the numerator and denominator are polynomial functions this function is a rational function.
has a variable in the denominator and the numerator and denominator are polynomial functions this function is a rational function.
Find the Domain of a Rational Function
Division by zero is undefined. Having a zero as the denominator is equivalent to division by zero thus is also undefined. The rational function is undefined for any value of the variable that gives a zero denominator. Find these values by creating an equation to solve. The equation is the expression in the denominator equal to zero.
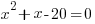 |
|
| Solve the equation. This equation is a quadratic equation and can be solved by factoring, completing the square or the quadratic formula. | 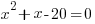 |
| Solve by factoring. Factor the expression on one side. | 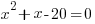 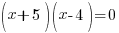 |
| Use the zero product property and set each factor equal to zero. | 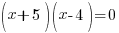 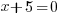 or or 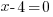 |
| Solve each equation. | 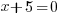 or or 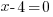 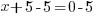 or or 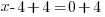 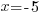 or or 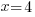 |
The values -5 and 4 give a zero value in the denominator, make the function undefined and must be excluded from the domain.
In set builder notation, the domain is 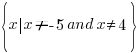
In interval notation, the domain is 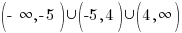
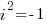
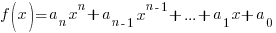
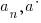 are from the real numbers.
are from the real numbers.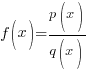
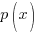 and
and 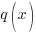 are polynomial functions and
are polynomial functions and