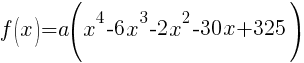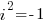Example: Form a polynomial f(x) with real coefficients having the given degree and zeros.
Degree 4; Zeros -2-3i; 5 multiplicity 2
Solution:
By the Fundamental Theorem of Algebra, since the degree of the polynomial is 4 the polynomial has 4 zeros if you count multiplicity.
There are three given zeros of -2-3i, 5, 5.
The remaining zero can be found using the Conjugate Pairs Theorem. f(x) is a polynomial with real coefficients. Since -2-3i is a complex zero of f(x) the conjugate pair of -2+3i is also a zero of f(x).
Now that all the zeros of f(x) are known the polynomial can be formed with the factors that are associated with each zero.
Since f(x) has a zero of 5, f(x) has a factor of x-5
Since f(x) has a second zero of 5, f(x) has a second factor of x-5
Since f(x) has a factor of -2-3i, f(x) has a factor of x-(-2-3i)
Since f(x) has a factor of -2+3i, f(x) has a factor of x-(-2+3i)
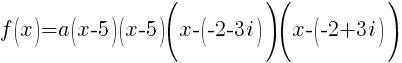 |
|
|
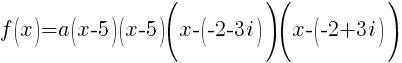 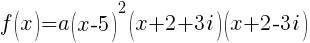 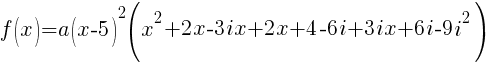 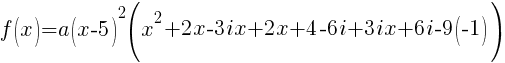 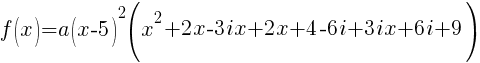 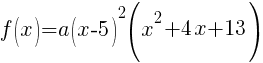 |
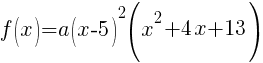 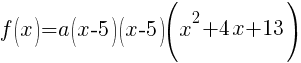 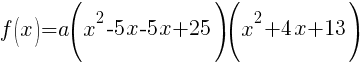 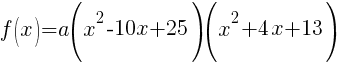 |
|
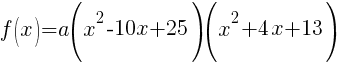 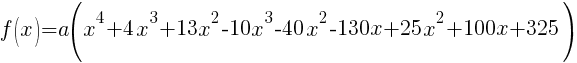 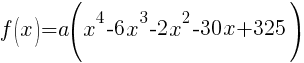 |
The polynomial with degree 4 and zeros of -2-3i and 5 wiht multiplicity 2 is