https://www.youtube.com/watch?v=0NUipZezwxE&feature=youtu.be
Category Archives: 5.2 The Real Zeros of a Polynomial Function
Polynomial Function: Finding Zeros and Write in Factored Form
Problem: Use the rational zeros theorem to find all real zeros of the polynomial function. Use the zeros to factor f over the real numbers.
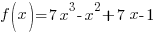
Since f is a polynomial function with integer coefficients use the rational zeros theorem to find the possible zeros.
The factors of the constant term, 1 are p.
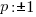
The factors of the leading coefficient, 7 are q.
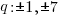
The possible rational zeros can be found by working out all of the possible combinations of p/q.
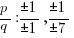
Simplifying these combinations give 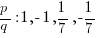
To test if any of these potential zeros are actual zeros, evaluate the function at these values.
This can be completed quickly using the ask feature in your calculator.




Since f(1/7) is zero, 1/7 is a zero of the function. Since the function has a zero of 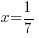 then the function has a factor of
then the function has a factor of 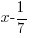
Use long division or synthetic division to to reduce the polynomial.
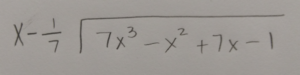 |
|
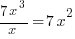 |
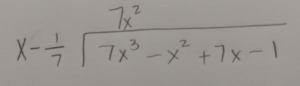 |
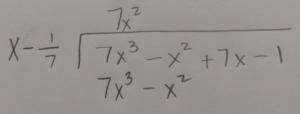 |
|
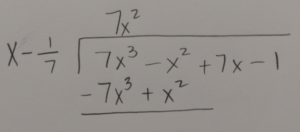 |
|
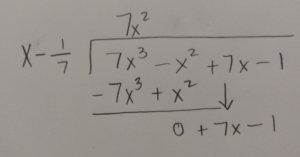 |
|
 |
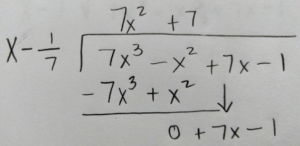 |
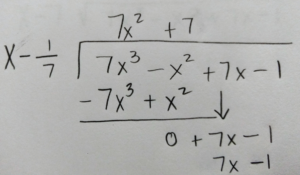 |
|
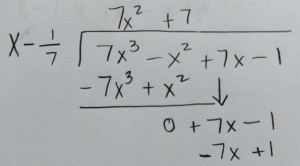 |
|
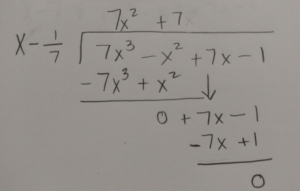 |
Write the function in factored form using the results of the long division.
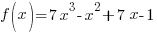
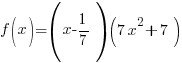
Factor completely.
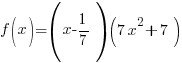
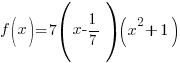
Intermediate Value Theorem
Problem: Use the Intermediate Value Theorem to show that the following function has a zero in the given interval. Approximate the zero to two decimal places.
![f(x)=9x^3+9x^2-9x+6; [-2,-1] f(x)=9x^3+9x^2-9x+6; [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_8c3d8866a3f884f4b90f75e40f6be143.png)
Solution:
To determine if there is a zero in the interval use the Intermediate Value theorem. To use the Intermediate Value Theorem, the function must be continuous on the interval ![[-2,-1] [-2,-1]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_ffd21cf987ccbaa47dd393edf5d2bd04.png) . The function
. The function 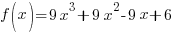 is a polynomial function and polynomial functions are defined and continuous for all real numbers.
is a polynomial function and polynomial functions are defined and continuous for all real numbers.
Evaluate the function at the endpoints and if there is a sign change. If there is a sign change, the Intermediate Value Theorem states there must be a zero on the interval. To evaluate the function at the endpoints, calculate 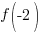 and
and 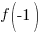 .
.
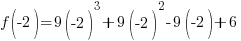
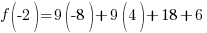
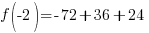
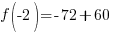
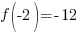
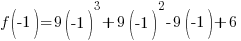
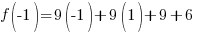
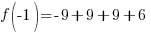
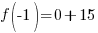
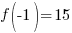
Since one endpoint gives a negative value and one endpoint gives a positive value, there must be a zero in the interval.
We can get a better approximation of the zero by trying to figure out the next decimal point. Write out all of the values to one decimal point between -2 and -1.
Fill the table. There are functions in your calculator that make this easier.



Use the Intermediate Value Theorem again. Look for a sign change. Looking down the table, there is a sign change between -1.8 and -1.7. With this information we now know the zero is between these two values.
Repeat this process again with two decimal places between -1.8 and -1.7.


Use the Intermediate Value Theorem. Look for a sign change. Looking down the table, there is a sign change between -1.78 and -1.77. With this information we now know the zero is between these two values and the zero to two decimal places is -1.77 since all the numbers between -1.78 and -1.77 start with -1.77.
Remainder Theorem and Factor Theorem
Problem: Use the remainder theorem to find the remainder when f(x) is divided by 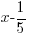 . Then use the factor theorem to determine whether
. Then use the factor theorem to determine whether 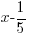 is a factor of f(x).
is a factor of f(x).
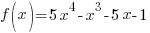
Solution:
The Remainder Theorem: Let f be a polynomial function. If 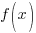 is divided by
is divided by 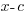 , then the remainder is
, then the remainder is 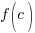 .
.
The remainder theorem gives a way to find the remainder without performing the division. The remainder when dividing by 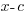 is
is 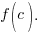 Calculate
Calculate 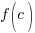 to find the remainder where c is the zero of the factor
to find the remainder where c is the zero of the factor 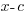 .
.
For the example above, f(x) is divided by 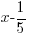 . The zero of the factor can be found by setting the factor equal to zero and solve.
. The zero of the factor can be found by setting the factor equal to zero and solve.
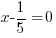
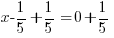
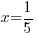
Use 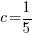 and calculate
and calculate 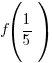 .
.
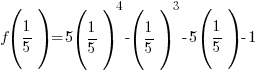
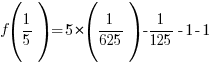
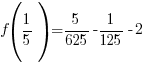
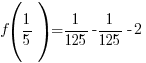
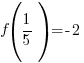
The remainder when f(x) is divided by 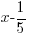 is -2.
is -2.
Factor Theorem: Let f be a polynomial function. Then 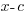 is a factor of f(x) if and only if
is a factor of f(x) if and only if 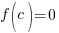 .
.
This theorem gives of the result that if 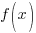 is divided by
is divided by 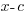 and the remainder is zero, then
and the remainder is zero, then 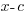 is a factor of f.
is a factor of f.
For the example above, the remainder when f(x) is divided by 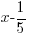 is -2. Since the remainder is not zero
is -2. Since the remainder is not zero 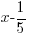 is not a factor.
is not a factor.