Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 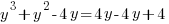 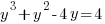 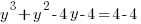 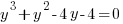 |
|
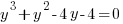 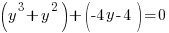 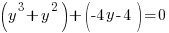 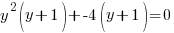 |
|
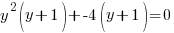 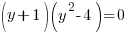 |
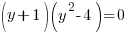 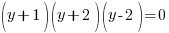 |
|
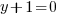 or or 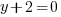 or or 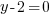 |
|
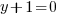 or or 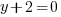 or or 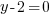 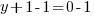 or or 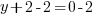 or or 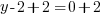 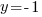 or or 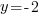 or or 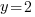 |
The solutions to the polynomial equation  are
are 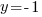 or
or 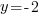 or
or 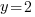 .
.
Example: Solve the polynomial equation

Solution: Solve the polynomial equation by factoring.
 |
|
|
 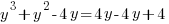 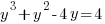 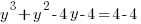 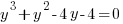 |
|
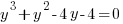 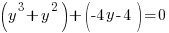 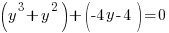 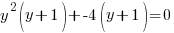 |
|
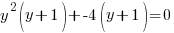 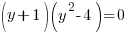 |
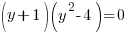 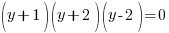 |
|
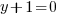 or or 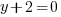 or or 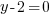 |
|
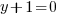 or or 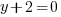 or or 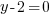 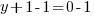 or or 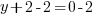 or or 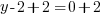 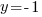 or or 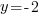 or or 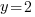 |
The solutions to the polynomial equation  are
are 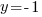 or
or 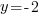 or
or 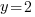 .
.