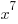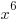Category Archives: 3.3 Properties of Functions

3.2 Properties of a Function's Graph, 3.3 Properties of Functions

Even, Odd, or Neither

Example: Determine if the function is even, odd, or neither.

f(x)=x^7+x^6

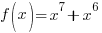
Background Knowledge:

For a function to be even it must fit the following definition.

f(- x)=f(x)

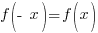
In words, this means that 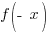f(- x) must equal the same expression as the original function.

For a function to be odd it must fit the following definition.

f(- x)=-f(x)

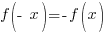
In words, this means that 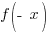f(- x) must equal the opposite expression as the original function.

We will calculate 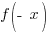f(- x)  for the given function and determine if it fits either definition.

Solution:

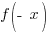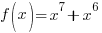We will calculate f(- x)  forf(x)=x^7+x^6 and determine if it fits either definition.

Calculate f(- x)
 f(- x)=(- x)^7+(- x)^6
Simplify (- x)^7.

  • Group the negatives. Since there are an odd number of negatives multiplied the product is negative.
  • Group the x’s.  Since the bases are the same, 7 x’s multiplied equals x^7
 f(- x)=(- x)^7+(- x)^6
f(- x)=(- x)(- x)(- x)(- x)(- x)(- x)(-x)+(- x)^6
f(- x)=-x^7+(- x)^6
Simplify (- x)^6.

  • Group the negatives. Since there are an even number of negatives multiplied the product is positive.
  • Group the x’s.  Since the bases are the same, 6 x’s multiplied equals x^6

 
f(- x)=-x^7+(- x)^6
f(- x)=-x^7+(- x)(- x)(- x)(- x)(- x)(- x)
f(- x)=-x^7+ x^6

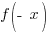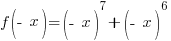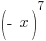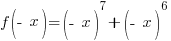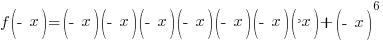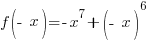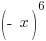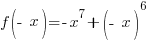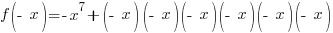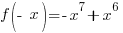Is the function even? No, 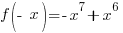 f(- x)=-x^7+ x^6 is not the same as the original function.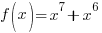 f(x)=x^7+x^6

Is the function odd? No, 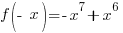f(- x)=-x^7+ x^6 is not the opposite of the original function.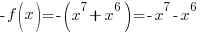 -f(x)=-(x^7+x^6)=-x^7-x^6

This function is not even or odd so we categorize it as “neither.”

YouTube Videos