Category Archives: 3.1 Functions
Set of Ordered Pairs: Is this a function?
Domain and Range from ordered Pairs
Finding Domain
Evaluating Functions
Finding Domain: Radical/Root Function (Even Root)
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
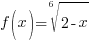
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 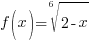 has a radical and the index is even. This function is a root function.
has a radical and the index is even. This function is a root function.
Find the Domain of a Root Function (Even Index)
Taking the even root of a negative number results in a complex or imaginary number. Since we are interested in real function values, we would like the expression inside the radical to be non-negative ( zero or positive) The root function is defined for any value of the variable where the expression under the radical is non-negative (zero or positive). Find these values by creating an inequality to solve. The inequality is the expression under the radical greater than or equal to zero.
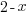 |
|
| Solve the inequality. This inequality is a linear inequality and can be solved by isolating the variable on one side. | 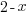 |
| Solve by isolating the variable. Start by subtracting 2 on both sides. | 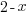 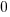 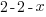 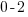 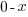 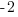 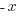 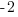 |
| Isolate the variable. Continue by dividing both sides by -1. Be sure to reverse the inequality symbol since you are dividing both sides by a negative. | 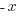 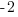 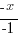 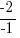 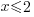 |
The function values where 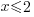 are defined for
are defined for 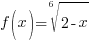 .
.
In set builder notation, the domain is ![]() .
.
In interval notation, the domain is (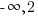 ]
]
Combination of Function: Evaluation of Division
Example:
Evaluate 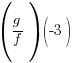 when
when 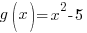 and
and 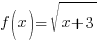
Solution:
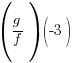 |
|
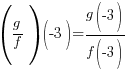 |
|
| Replace x with -3 in each function | 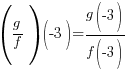 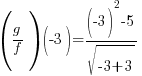 |
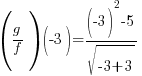 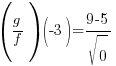 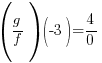 |
|
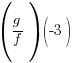 is undefined is undefined |
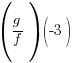 is undefined.
is undefined.
Finding Domain: Rational Function
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
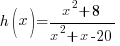
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 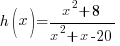 has a variable in the denominator and the numerator and denominator are polynomial functions this function is a rational function.
has a variable in the denominator and the numerator and denominator are polynomial functions this function is a rational function.
Find the Domain of a Rational Function
Division by zero is undefined. Having a zero as the denominator is equivalent to division by zero thus is also undefined. The rational function is undefined for any value of the variable that gives a zero denominator. Find these values by creating an equation to solve. The equation is the expression in the denominator equal to zero.
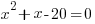 |
|
| Solve the equation. This equation is a quadratic equation and can be solved by factoring, completing the square or the quadratic formula. | 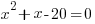 |
| Solve by factoring. Factor the expression on one side. | 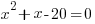 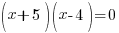 |
| Use the zero product property and set each factor equal to zero. | 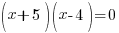 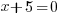 or or 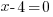 |
| Solve each equation. | 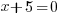 or or 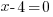 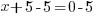 or or 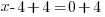 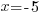 or or 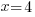 |
The values -5 and 4 give a zero value in the denominator, make the function undefined and must be excluded from the domain.
In set builder notation, the domain is 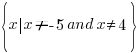
In interval notation, the domain is 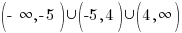
Difference Quotient: Quadratic Function
Example: Find the difference quotient for 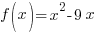
The Difference Quotient: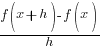
Solution:
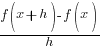 |
|
| Write the difference quotient for the given function | 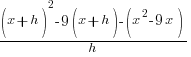 |
| Apply the exponent and use the distributive property | 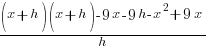 |
| Multiply | 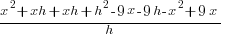 |
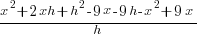 |
|
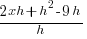 |
|
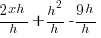 |
|
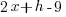 |
Difference Quotient: Rational Function
Example: Find the difference quotient for 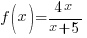
The Difference Quotient: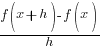
Solution:
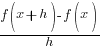 |
|
| Write the difference quotient for the given function | 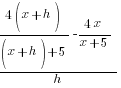 |
| Use the distributive property | 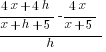 |
| Simplify the complex fraction by multiplying the numerator and denominator by the common denominator | 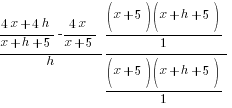 |
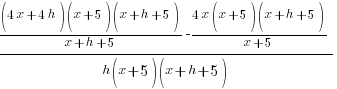 |
|
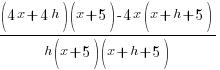 |
|
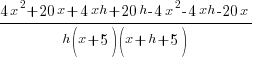 |
|
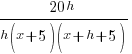 |
|
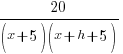 |
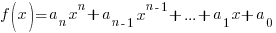
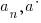 are from the real numbers.
are from the real numbers.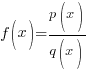
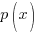 and
and 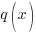 are polynomial functions and
are polynomial functions and