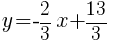Category Archives: Sullivan Chapter 2
Finding the Equation of a Line: Given a parallel line in standard form and a point on the line
Circle: Find General Form from Standard Form
Example: Find the general form of the circle
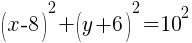
Solution:
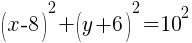
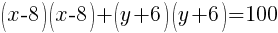
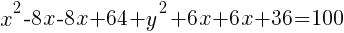
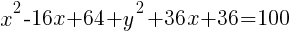
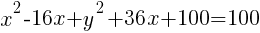
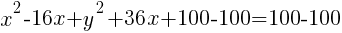
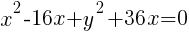
Forms of Linear Equations
Slope Intercept Form
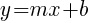
m is the slope of the line and 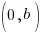 is the y-intercept
is the y-intercept
Point Slope Form
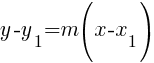
m is the slope of the line and 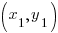 is a point on the line.
is a point on the line.
Standard Form of a Line
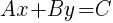
Graphing Linear Equations with Slope Intercept Form
Example: Graph the linear equation using the slope and the y-intercept. (the slope is positive and fractional)
Example: Graph the linear equation using the slope and the y-intercept. (positive and negative fractional slopes)
Example: Graph the linear equation using the slope and the y-intercept. (equation written in standard form)
Graphing Horizontal and Vertical Lines
Perpendicular Lines and Parallel Lines
Example: What are parallel and perpendicular lines?
Example: How are the slopes of parallel and perpendicular lines related? (only watch until 1 min 20 seconds)
Example: Are the lines parallel, perpendicular or neither?
Example: Are the lines perpendicular to each other?
Finding the equation of a line perpendicular to another line
Example: Write the equation of a line in point-slope form passing through the point 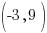 and perpendicular to the line whose equation is
and perpendicular to the line whose equation is 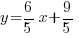 .
.
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 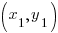 is a point on the line.
is a point on the line.
Point-slope formula: 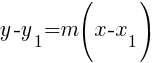
Although the slope of the line is not given, the slope can be deducted from the line being perpendicular to 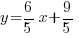 .
.
Perpendicular lines have negative reciprocal slopes. Since the slope of the given line is 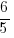 , the slope of the perpendicular line
, the slope of the perpendicular line 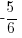 .
.
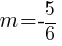 and
and 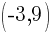
Substitute the values into the point-slope formula.
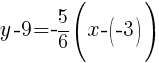
The point-slope form of the line is as follows.
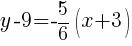
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope intercept form)
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope standard form)
Example: Find the equation of a line perpendicular to the x-axis.
Example: Find the equation of a line perpendicular to the x-axis and perpendicular to the y-axis.
Finding the Equation of a Line parallel to another line
Example: Find the equation of the line parallel to another line and passing through a specific point. (parallel equation in slope intercept form)
Example: Find the equation of the line parallel to another line and passing though a specific point. (parallel line in standard form)
Example: Find the equation of the line parallel to the x-axis or y-axis and passing through a specific point.
Example: What is an equation parallel to the y-axis?
Example: What is an equation parallel to the x-axis?
Finding the Equation of a line given a fractional slope and a point
Example: Find the equation of a line in slope intercept form given the slope of the line is 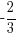 and the line passes through the point
and the line passes through the point 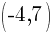
Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and 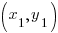 is a point on the line.
is a point on the line.
Point-slope formula: 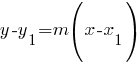
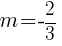 and
and 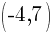
Substitute the values into the formula.
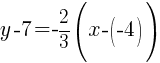
Since the instructions ask to write the equation in slope intercept form 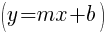 we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
we will simplify and write the equation with y by itself on one side. I will also use the clearing fractions method to avoid having to add fractions.
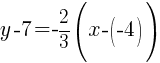
![3(y-7) = 3[-{2/3}(x+4)] 3(y-7) = 3[-{2/3}(x+4)]](https://math15fun.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980_0233a6f7265fc4d6a65d52d25e31bbd1.png) (Multiply by LCM)
(Multiply by LCM)
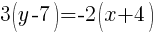 (Cancel Denominator)
(Cancel Denominator)
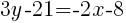
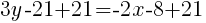
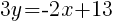
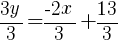
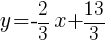
The equation of a line in slope intercept form with a slope of 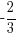 and passing through the point
and passing through the point 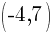 is
is