Problem:

Benjamin & Associates, a real estate developer, recently built condominiums in McCall, Idaho.  The condos were either two-bedroom units or three-bedroom units.  If the total number of bedrooms in the entire complex is 498, how many two-bedroom units are there?  How many three-bedroom units are there?

Solution:

Assign variables to the values we are looking for in the equation.

Let x be the number of two-bedroom units.
Let y be the number of three-bedroom units.

Create equations using the information given in the problem.

Since there are 199 condos built in the complex, the number of two-bedroom units plus the three bedroom units should equal the total units of 199.

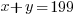
Since there are a total of 498 bedrooms in the complex, 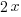represents number of bedrooms coming from two-bedroom units, and 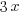represents number of bedrooms coming from three-bedroom units,  the number of bedrooms from two-bedroom units plus the number of bedrooms from three-bedroom units should equal to the total number of bedrooms of 498.

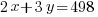
Solve the system of equations.

Solve one equation for one of the variables.  Choose to solve for x in the first equation since it doesn’t have a coefficient and fractions can be avoided that way.
Substitute the expression into the other equation.
Solve for the other variable.  Use the distributive property to remove parenthesis. Combine like terms Isolate the variable on one side of the equation

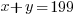
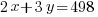
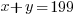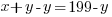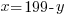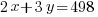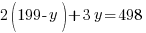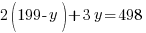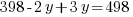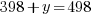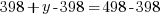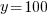y represents the number of three-bedroom units.  There are 100 three-bedroom units.

x represents the number of two-bedroom units.  There are 199-100=99 two-bedroom units.

https://www.youtube.com/watch?v=8kRG7jlBMAY