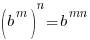Category Archives: Trigsted Chapter 5
Converting an Exponential Equation to a Logarithmic Equation
Periodic and Continuous Compound Interest
Solve an Exponential Equation: Relating the Bases
Problem: Solve the exponential equation.
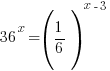
Solution:
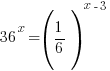 |
|
The bases of the exponents on each side of the equation can be made the same. 36 can be written as 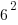 and and 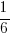 can be written as can be written as 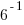 |
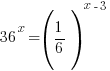 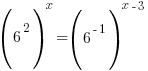 |
|
Use the power rule for exponents to multiply the exponents. |
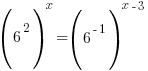 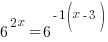 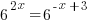 |
| Exponential functions are one-to-one thus giving us the property that if the bases are the same the exponents are equal. If 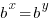 then then 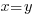 |
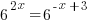 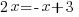 |
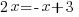 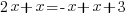 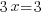
|
|
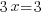 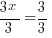  |
|
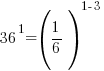 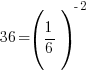 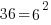 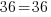 |
The solution to the equation 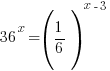 is
is  .
.
Here is a video example of a similar type of problem.
Condense a Logarithm
Problem: Use the properties of logarithms to rewrite the expression as a single logarithm. Whenever possible, evaluate logarithmic expressions.
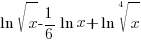
Soluton:
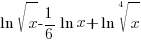 |
|
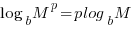 |
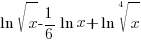 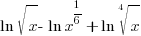 |
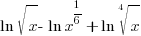 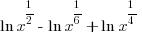 |
|
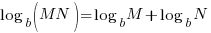 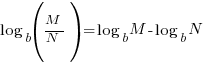 |
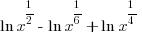 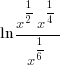 |
| Since these base of the exponential expressions are the same, combine using the power and quotient rules for exponent. Product Rule for Exponents: 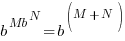 Quotient Rule for Exponents: 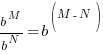 |
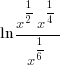 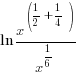 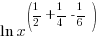 |
| Find a common denominator to combine the fractions. | 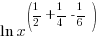 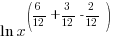 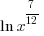 |
Here is a video with a similar example worked out.
Application: Exponential Growth and Decay (Half-life)
Example: The half life of radium is 1690 years. If 50 grams are present now, how much will be present in 630 years?
Solution: There is a two part process to this problem. Part 1: Use some of the information to find the decay rate of radium. Part 2: Answer the question using the rest of the given information.
Part 1: Find the decay rate of radium.
Since we are using an exponential model for this problem we should be clear on the parts of the exponential decay model.
Exponential Decay Model
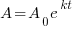
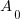 is the initial amount
is the initial amount
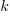 is the decay rate
is the decay rate
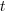 is the time
is the time
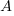 is the amount after t time has passed
is the amount after t time has passed
Since radium has a half life of 1690 years, we know that after 1690 years there will be half of the initial amount of radium left. This allows me to establish a relationship between the initial amount and the amount after 1690. The amount after 1690 year is half of the initial amount. 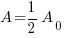 when the
when the 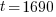 .
.
Substitute these values into the exponential decay formula and solve for k.
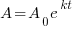 |
|
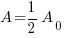 and and 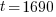 |
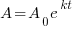 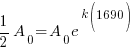 |
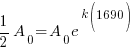 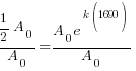 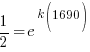 |
|
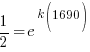 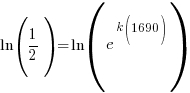 |
|
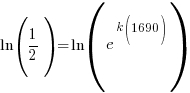 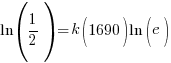 |
|
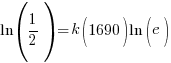 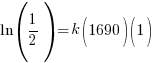 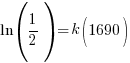 |
|
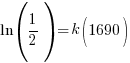 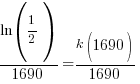 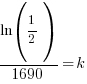 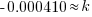 |
Using only the information about radium having a half-life of 1690 years I have found the decay rate for radium.
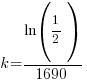
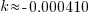
Note: Although I have put an approximation for k here, try not to round until the very last step.
Part 2: Answer the question using the rest of the given information.
Given information: If 50 grams are present now, how much will be present in 630 years?
With this information I can identify the initial amount of radium as 50 grams and the time to be 630 years. Symbolically that is 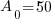 when the
when the 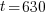 . Substitute the given information and the decay rate k found in part 1 to the exponential decay formula.
. Substitute the given information and the decay rate k found in part 1 to the exponential decay formula.
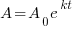 |
|
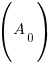 , time (t), and the decay rate (k). , time (t), and the decay rate (k).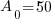 , , 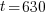 , and , and 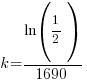 |
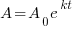 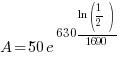 |
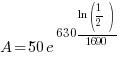 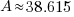 |
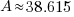
38.615 grams will be present 630 years later is 50 grams are present initially.
Here is a video example that is similar to the above example and it shows how to enter information in the calculator.
Application of Exponential Functions: Finding the Interest Rate
Example:
What is the interest rate necessary for an investment to quadruple after 7 year of continuous compound interest?
Solution:
Since this question involve continuous compound interest, we will use the associated formula.
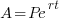
We are given that the invest quadruples in 7 years. This tells me that when t=7 that A will be 4 times P. I can write that in symbols A=4P.
Substitute these values into the continuous compound formula and solve for the interest rate.
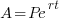 |
|
| Substitute the values of t and A into the formula | 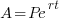 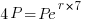 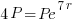 |
| Solve for r by dividing both sides by P and simplifying | 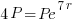 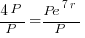 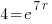 |
| Solve for r by taking the log of both sides. | 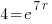 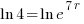 |
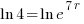 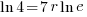 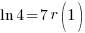 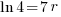 |
|
| Solve for r by dividing both sides by 7 and simplifying | 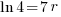 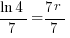 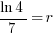 |
| Find the value in the calculator | 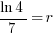 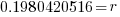 |
| Write the answer as a percentage rounded to two decimal places | 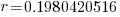 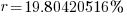 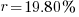 |
Solve an exponential equation: Take the log of both sides
Example:
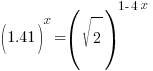
Solution:
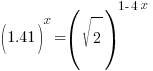 |
|
| Since the bases cannot be easily written the same use the method of taking the log of both sides | 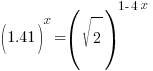 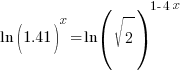 |
| Use the power rule for logarithms | 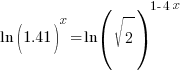 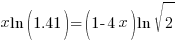 |
| Use the distributive law | 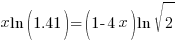 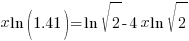 |
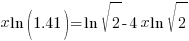 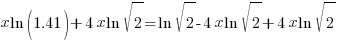 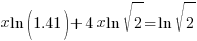 |
|
| Factor the common x | 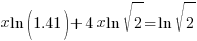 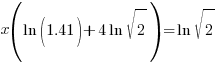 |
| Solve for x by dividing both sides by the factor in the parenthesis and simplify | 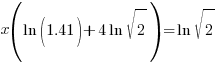 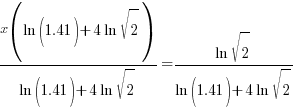 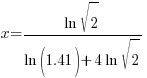 |
| The solution | 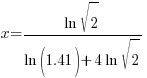 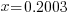 |
When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator. Here is an example of how you might enter it.
(ln (sqrt{2}))/(ln(1.41)+4 ln(sqrt{2}))
Here is a youtube video with a similar example.
Solve the Logarithmic Equation by the one to one property
Example:
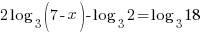
Solution:
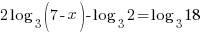 |
|
| Use the power rule and the quotient rule to condense to a single logarithm | 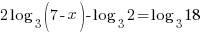 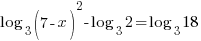 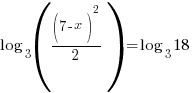 |
| Since both sides of the equation have the same log base the expressions inside the logarithms must be equal | 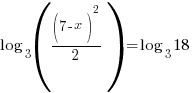 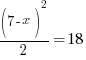 |
| Clear the denominator by multiplying by 2 on both sides and simplifying | 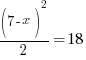 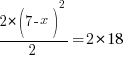 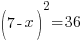 |
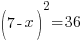 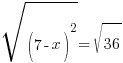 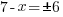 |
|
| Get x by itself by subtracting 7 on both sides | 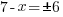 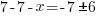 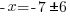 |
| Get x by itself by dividing both sides by negative 1 | 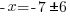 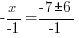 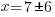 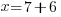 or or 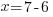 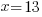 or or  |
| Check x=13 | 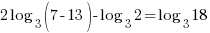 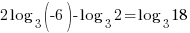 |
| Check x=1 | 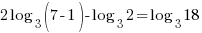 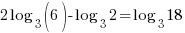 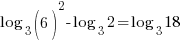 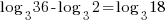 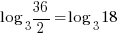 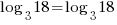 |
The solution to the equation is x=1.
Here is a youtube video that is similar.
Solve an Exponential Equation: Take the log of both sides
Problem: Solve the exponential equation.
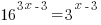
Solution:
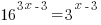 |
|
| Since the bases cannot be easily written the same, use the method of taking the log of both sides | 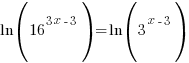 |
| Use the power rule for logarithms. | 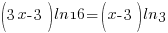 |
| Use the distributive property. | 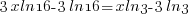 |
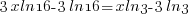 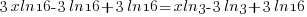 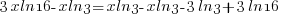 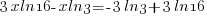 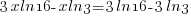 |
|
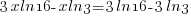 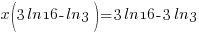 |
|
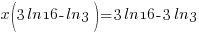 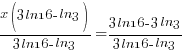 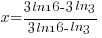 |
|
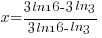 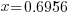 |
When you type this into a calculator be sure to use parenthesis around the numerator and around the denominator. Here is an example of how you might enter it.
(3ln(16)-3ln(3))/(3ln(16)-ln(3))