Category Archives: Trigsted Chapter 5
Converting a Logarithmic Equations to an Exponential Equation
Exponential Equations: Same Base
Application: Exponential Growth
Application: Exponential Growth and Decay
Application: Exponential Growth
Graphing Exponential Functions (Base e)
Graphing an Exponential Function (Base Function)
Exponents: Simplify
Example: Rewrite the expression in the form 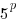 where p is an algebraic expression.
where p is an algebraic expression.
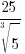
Solution:
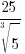 |
|
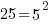 |
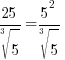 |
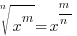 . For this example . For this example 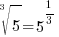 |
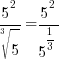 |
Quotient Rule for Exponents 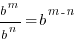 |
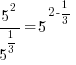 |
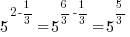 |
Application of Exponential Functions: Doubling Time
Example:
How long does it take for an investment to double if it is invested at 18% compounded continuously?
Solution:
Since this question involve continuous compound interest, we will use the associated formula.
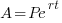
We are given that the interest rate is 18% or 0.18. This tells me that when r=0.18 Since we are looking for the doubling time, A will be 2 times P. I can write that in symbols A=2P.
Substitute these values into the continuous compound formula and solve for the interest rate.
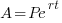 |
|
| Substitute the values of r and A into the formula | 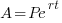 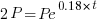 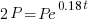 |
| Solve for t by dividing both sides by P and simplifying | 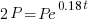 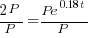 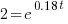 |
| Solve for t by taking the log of both sides. | 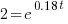 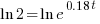 |
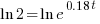 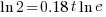 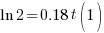 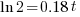 |
|
| Solve for t by dividing both sides by 0.18 and simplifying | 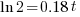 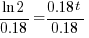 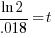 |
| Find the value in the calculator | 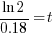 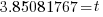 |
| Write the answer rounded to two decimal places | 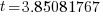 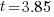 |
It will take 3.85 years to double your money when interest is compounded continuously at 18%.
If you need to write this in years and months, you will need to convert the 0.85 to months. Since there are 12 months in a year, multiply 0.85 by 12 to get 10.2. I will round to the nearest months to get 10.
It will take 3 years and 10 months to double your money when interest is compounded continuously at 18%.
Here is a video that is similar except that you are looking for the investment to triple.