Category Archives: Trigsted Chapter 3
Finding Domain and Range from the Graph
Evaluating Functions
Finding Function Values from the graph
Here are some practice problems so you can try it yourself.
Finding Domain: Radical/Root Function (Even Root)
Example: Classify the function as a polynomial function, rational function, or root function, and then find the domain. Write the domain interval notation and set builder notation.
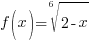
Solution:
Classify the Function
| Polynomial Function
A polynomial function is a function of the form
where n is a non-negative integer {0, 1, 2, 3, 4, …} and the coefficients |
|
| Rational Function
A rational function is a function of the form
where |
|
| Root Function (even index)
A root function is a function of the form
where n is an even positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an even number. {2, 4, 6, 8, …} The square root is an even index although the index is not written. |
| Root Function (odd index)
A root function is a function of the form
where n is an odd positive integer greater than or equal to 2. |
The variable is inside or underneath a radical. The index of the radical is an odd number. {3, 5, 7, 9, …} The cube root is an odd index. |
Since the function 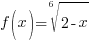 has a radical and the index is even. This function is a root function.
has a radical and the index is even. This function is a root function.
Find the Domain of a Root Function (Even Index)
Taking the even root of a negative number results in a complex or imaginary number. Since we are interested in real function values, we would like the expression inside the radical to be non-negative ( zero or positive) The root function is defined for any value of the variable where the expression under the radical is non-negative (zero or positive). Find these values by creating an inequality to solve. The inequality is the expression under the radical greater than or equal to zero.
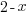 |
|
| Solve the inequality. This inequality is a linear inequality and can be solved by isolating the variable on one side. | 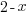 |
| Solve by isolating the variable. Start by subtracting 2 on both sides. | 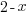 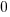 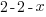 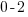 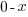 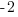 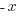 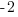 |
| Isolate the variable. Continue by dividing both sides by -1. Be sure to reverse the inequality symbol since you are dividing both sides by a negative. | 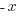 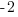 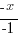 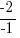 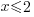 |
The function values where 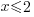 are defined for
are defined for 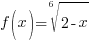 .
.
In set builder notation, the domain is ![]() .
.
In interval notation, the domain is (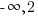 ]
]
Graphing by Transformations: Quadratic
Example: For the function below. Graph using transformations.
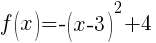
First we must examine the base function 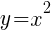
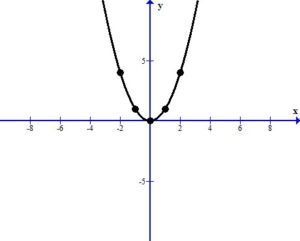
Graph using plotting points. We can use the standard set of x-values to find ordered pairs. Substitute the standard set of x-values into the base function to get the base graph.
| x | y |
|---|---|
| -2 | (-2)^2=4 |
| -1 | (-1)^2=1 |
| 0 | (0)^2=0 |
| 1 | (1)^2=1 |
| 2 | (2)^2=4 |
The graph below shows the points plotted and the line that connects them. The domain is 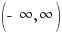 and the range is [
and the range is [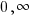 )
)
Analyze the transformations.
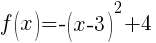
The -3 inside the square shifts the graph right 3 units.
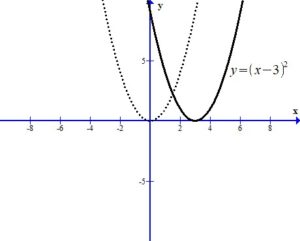
The – in the front of the base reflects the graph over the x-axis.
The +4 outside the square shifts the graph up 4 units.
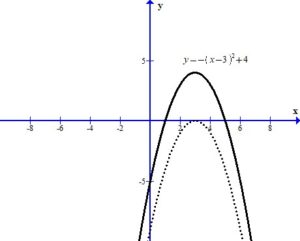
You can see the graph after the transformations.
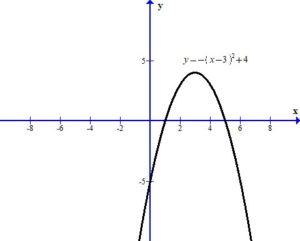
The domain is 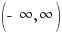 and the range is (
and the range is (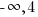 ]
]
Here is a video example of a transformation of a square function.
Verifying Two Functions are Inverses
Finding the Inverse of a Linear Function
Combination of Function: Evaluation of Division
Example:
Evaluate 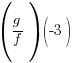 when
when 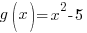 and
and 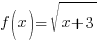
Solution:
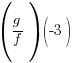 |
|
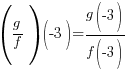 |
|
| Replace x with -3 in each function | 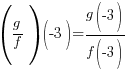 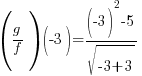 |
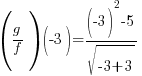 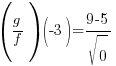 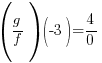 |
|
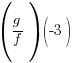 is undefined is undefined |
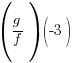 is undefined.
is undefined.
Composition of Functions
Example:
Find 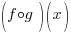 when
when
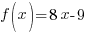 and
and 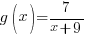
Solution:
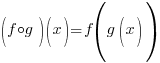 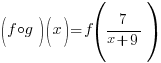 |
|
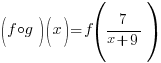 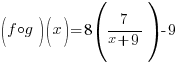 |
|
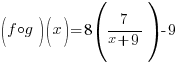 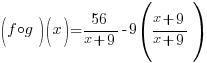 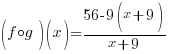 |
|
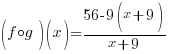 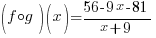 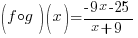 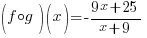 |
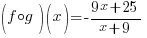
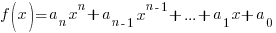
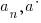 are from the real numbers.
are from the real numbers.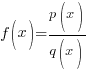
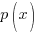 and
and 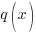 are polynomial functions and
are polynomial functions and