Category Archives: 2.4 Parallel and Perpendicular Lines
Perpendicular Lines and Parallel Lines
Example: What are parallel and perpendicular lines?
Example: How are the slopes of parallel and perpendicular lines related? (only watch until 1 min 20 seconds)
Example: Are the lines parallel, perpendicular or neither?
Example: Are the lines perpendicular to each other?
Finding the equation of a line perpendicular to another line
Example: Write the equation of a line in point-slope form passing through the point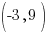 
and perpendicular to the line whose equation is 
.
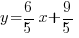Solution:
Use the point-slope formula of the line to start building the line. m represents the slope of the line and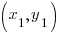 
is a point on the line.
Point-slope formula: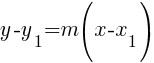 
Although the slope of the line is not given, the slope can be deducted from the line being perpendicular to .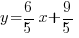
Perpendicular lines have negative reciprocal slopes. Since the slope of the given line is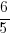 
, the slope of the perpendicular line 
.
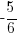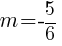and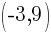 
Substitute the values into the point-slope formula.
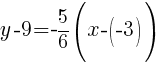
The point-slope form of the line is as follows.
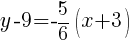
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope intercept form)
Example: Find the equation of a line perpendicular to another line and passing through a specific point. (The other line in slope standard form)
Example: Find the equation of a line perpendicular to the x-axis.
Example: Find the equation of a line perpendicular to the x-axis and perpendicular to the y-axis.
Finding the Equation of a Line parallel to another line
Example: Find the equation of the line parallel to another line and passing through a specific point. (parallel equation in slope intercept form)
Example: Find the equation of the line parallel to another line and passing though a specific point. (parallel line in standard form)
Example: Find the equation of the line parallel to the x-axis or y-axis and passing through a specific point.
Example: What is an equation parallel to the y-axis?
Example: What is an equation parallel to the x-axis?