Practice Problems
Addition and Multiplication Principles Combined
Solutions to Practice Problems
Example: Solve the quadratic equation by completing the square
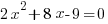
Solution:
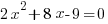 |
|
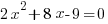 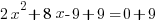 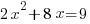 |
|
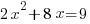 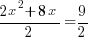 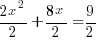 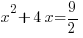 |
|
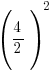 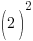 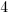 |
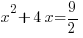 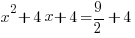 |
| The left hand side factors to be a perfect square | 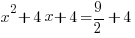 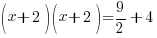 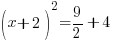 |
| Simplify the right hand side by finding a common denominator and adding the fractions. | 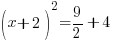 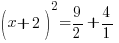 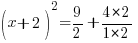 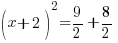 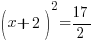 |
| Solve the equation using the square root method. Start by taking the square root of both sides to get rid of the square | 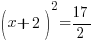 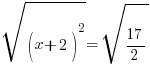 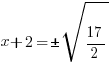 |
| Solve for x by subtracting 2 from both sides. | 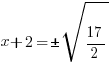 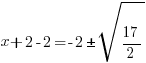 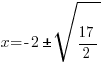 |
| Rationalize the denominator by applying the radical to the numerator and denominator | 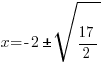 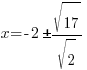 |
Rationalize the denominator by multiplying by the fraction 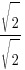 |
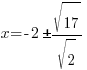 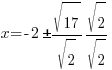 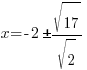 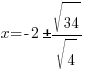 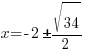 |
https://www.youtube.com/watch?v=tHxc3fO8yOo
Example: Solve the equation.
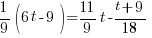
Solution:
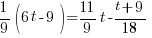 |
|
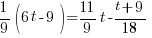 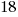 * *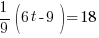 * *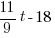 * *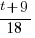 |
|
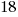 * *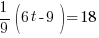 * *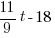 * *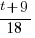 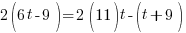 |
|
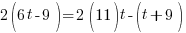 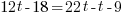 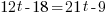 |
|
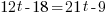 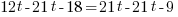 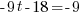 |
|
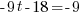 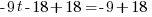 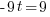 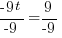 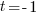 |
The solution to the equation is -1.
Here is a youtube video that might help as well.
Example: The product of some negative number and 5 less than twice that number is 273. Find the number.
Solution: Translate the statement into an equation and then solve the equation.
“The product of some negative number…”
Let x be some negative number and multiply that number by the expression that comes next in the statement.
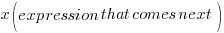
“…and 5 less than twice that number…”
5 less than means take 5 away from what follows. Twice that number refers to 2 times the negative number that was described before. (2x-5)
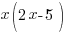
“…is 273”
This translates to equals 273.
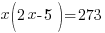
Solve the equation.
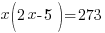 |
|
| Use the distributed property to rewrite the equation (recognize that the equation is a quadratic equation) | 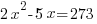 |
| Choose the method for solving the quadratic equation (factoring, square root method, completing the square or quadratic formula) I will demonstrate factoring so I need to move all terms to the same side to have zero on one side. | 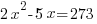 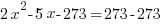 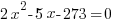 |
| Factor | 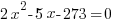 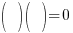 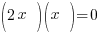 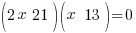 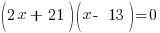 |
| Use the zero product property and set each factor equal to zero and solve. | 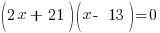 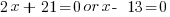 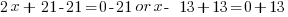 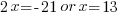 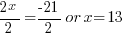 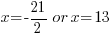 |
Since the statement says that the number is negative, the number is 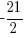 .
.
Example: Larry invested part of his $31,000 advance at 6% annual simple interest and the rest at 5% annual simple interest. If his total yearly interest from both accounts was $1,760, find the amount invested at each rate.
Solution: This question involved simple interest. We will use the simple interest formula.
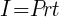
The I stands for interest, the P stands for principal (initial investment), r stands for the interest rate and t stands for time in years.
When starting an application problem like this it can be helpful to organize the information in a table using the formula.
| I | P | r | t | |
| 6% Account | ||||
| 5% Account |
Begin filling in the information from the problem. The interest rate is the most obvious and you should use the decimal version of the percent by moving the decimal place left two places. Since the problem state that $1760 is the yearly interest for both accounts, we will use a time of 1 year.
| I | P | r | t | |
| 6% Account | .06 | 1 | ||
| 5% Account | .05 | 1 |
The goal in this question is to find the amount invested in each account. I will let x be the amount invested in the 6% account. The problem states that the rest of the $31,000 will be invested in the 5% account. We can represent the rest of the money as 31000-x.
| I | P | r | t | |
| 6% Account | x | .06 | 1 | |
| 5% Account | 31000-x | .05 | 1 |
You can fill in the interest column using the simple interest formula.
For the 6% account: 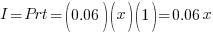
For the 5% account: 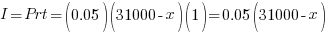
| I | P | r | t | |
| 6% Account | 0 .06x | x | 0.06 | 1 |
| 5% Account | 0.05(31000-x) | 31000-x | 0.05 | 1 |
You can now create an equation with this information. The interest from the first account plus the interest from the second account should equal the total interest of $1760.
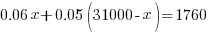
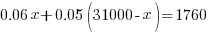 |
|
| Use the distributive property and combine like terms to simplify each side of the equation. | 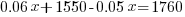 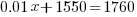 |
| Solve for x by subtracting 1550 on both sides and simplifying. | 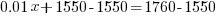 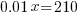 |
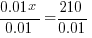 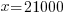 |
Since x represents the amount invested in the 6% account, $21000 is invested in the 6% account and the rest is invested in the 5% account. The rest is $31,000-$21,000=$10,000. $10,000 is invested in the 5% account.
Video Example:
Example: Solve the rational equation.
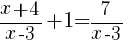
Solution:
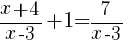
Since we are solving a rational equation we need to first find the restrictions (the values of x that cause the expression to be undefined).
To find the restrictions create an equation by setting each denominator equal to zero and solving.
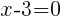
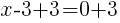
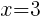
Having x=3 causes a zero in the denominator and the overall expression undefined. That makes 3 a restricted value .
With the restriction in mind we will solve the equation.
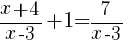 |
|
Multiply each side of the equation by the least common multiple of the denominators. For this equation the least common multiple is 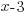 |
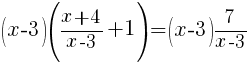 |
| Distribute the least common multiple to each term. | 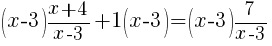 |
| Simplify by canceling the common factors. This should clear any denominators. | 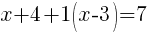 |
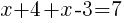 |
|
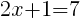 |
|
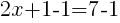 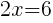 |
|
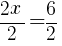 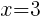 |
|
Video Example:
Example: Solve the equation.
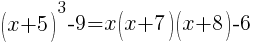
Solution:
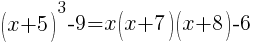 |
|
| Simplify both sides of the equation. On the left hand side, rewrite the exponent. On the right hand side, begin to simplify the multiplication. | 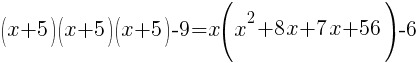 |
| Simplify both sides of the equation. On the left hand side, begin multiplying. On the right hand side, combine like terms. | 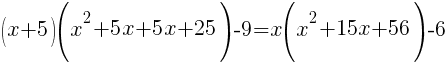 |
| Simplify both sides of the equation. On the left hand side, combine like terms. On the right hand side use the distributive property. | 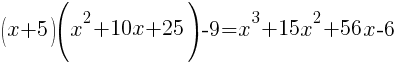 |
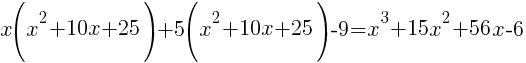 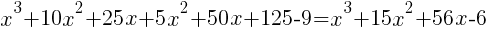 |
|
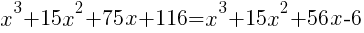 |
|
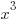 from each side. It cancels from each side. from each side. It cancels from each side. |
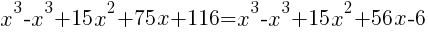 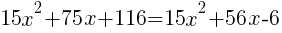 |
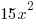 from each side. It cancels from each side. from each side. It cancels from each side. |
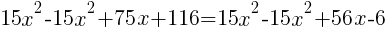 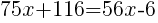 |
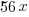 from each side and simplify. from each side and simplify. |
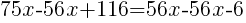 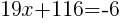 |
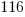 from each side and simplify. from each side and simplify. |
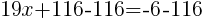 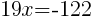 |
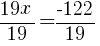 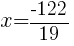 |
Example: Solve the equation.
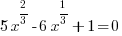
Solution:
The equation is similar to a quadratic. It has 3 terms and one exponent is twice the other. Since the equation is quadratic in form, use substitution to solve the equation.
Use the following substitution to rewrite the equation
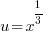
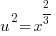
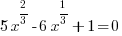 |
|
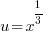 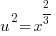 |
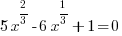 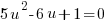 |
1) Factor the quadratic |
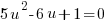 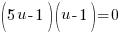 |
2) Apply the zero product property |
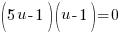 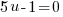 or or 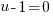 |
3) Solve each linear factor |
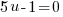 or or 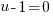 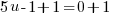 or or 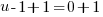 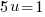 or or 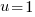 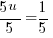 or or 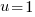 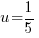 or or 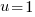 |
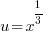 |
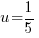 or or 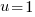 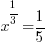 or or 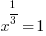
|
| Solve the equation with rational exponents. 1) Rewrite the rational exponents in radical form |
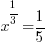 or or 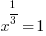 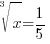 or or 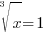 |
| Solve the equation with rational exponents. 2) Cancel the cube root by cubing both sides. 3) Simplify |
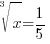 or or 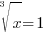 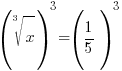 or or 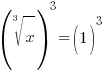 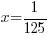 or or  |
The solution to 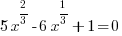 is
is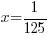 or
or  .
.
Here is a video with similar examples.