Category Archives: Trigsted Chapter 1
Polynomial Inequalities
Absolute Value Inequalities
Absolute Value Equations
Solving Linear Inequalities
https://www.youtube.com/watch?v=0X-bMeIN53I
Example with Fractions
Interval Notation
Simplifying Radicals
Multiplying Complex Conjugates
Rational Equation
Example: Solve the rational equation.
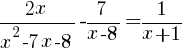
Solution:
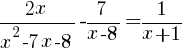
Since we are solving a rational equation we need to first find the restrictions (the values of x that cause the expression to be undefined).
To find the restrictions create an equation by setting each denominator equal to zero and solving.
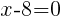
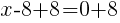
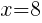
Having x=8 causes a zero in the denominator and the overall expression undefined. That makes 8 a restricted value .
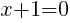
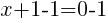
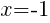
Having x=-1 causes a zero in the denominator and the overall expression undefined. That makes -1 a restricted value .
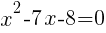
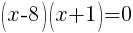
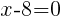 or
or 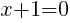
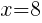 or
or 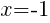
This gives the same restrictions we have already accounted for.
With the restriction in mind we will solve the equation.
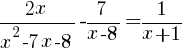 |
|
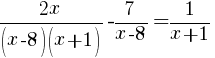 |
|
Multiply each side of the equation by the least common multiple of the denominators. For this equation the least common multiple is 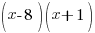 |
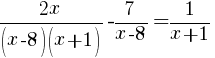 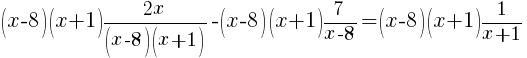 |
| Simplify by canceling the common factors. This should clear any denominators. | 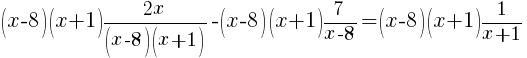 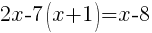 |
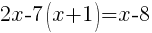 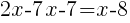 |
|
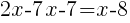 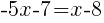 |
|
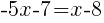 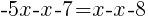 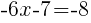 |
|
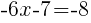 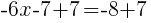 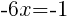 |
|
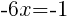 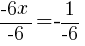 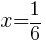 |
|
Video Example:
Solve a Linear Equation: Clearing Decimals
https://www.youtube.com/watch?v=AY8kS_BjCfE