Category Archives: 1.8 Absolute Value Equations and Inequalities

1.8 Absolute Value Equations and Inequalities

Absolute Value Inequality: Less than or less than or equal to

Example: Solve the inequality.  Express the solution using interval notation.

delim{|}{12-4x}{|}<=3

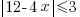
Solution:

Original absolute value inequality
delim{|}{12-4x}{|}<=3
Since the absolute value is isolated, get rid of the absolute value by writing the equivalent compound inequality.
delim{|}{12-4x}{|}<=3
-3<=12-4x<=3
Solve the compound inequality by isolating the x in the middle. Start by subtracting 12 from each part.
-3<=12-4x<=3
-3-12<=12-12-4x<=3-12
-15<=-4x<=-9
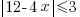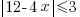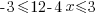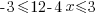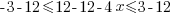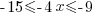Isolating the x in the middle: Divide by -4 on each part.
Note: Reverse the inequality symbol when dividing by a negative.  Reversing the order of the numbers is equivalent to reversing the signs.
-15<=-4x<=-9
{-9}/{-4}<={-4x}/{-4}<={-15}/{-4}
9/4 <=x <=15/4
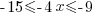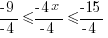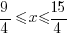Write the interval notation for the inequality.
[9/4,15/4]