Example: Solve the quadratic equation with the quadratic formula.
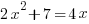
Solution:
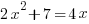 |
|
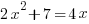 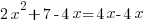 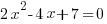 |
|
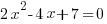 |
|
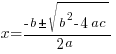 |
|
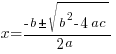 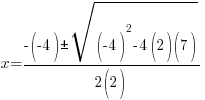 |
|
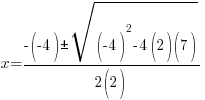 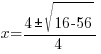 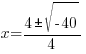 |
|
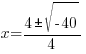 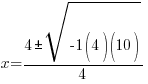 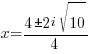 |
|
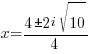 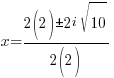 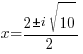 |
The solutions to the quadratic equation are 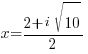 and
and 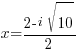 .
.
Example: Solve the quadratic equation with the quadratic formula.
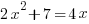
Solution:
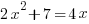 |
|
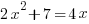 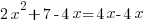 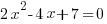 |
|
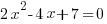 |
|
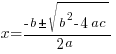 |
|
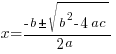 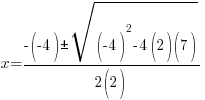 |
|
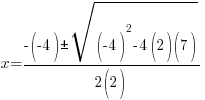 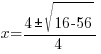 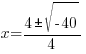 |
|
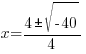 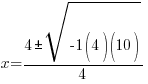 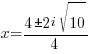 |
|
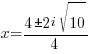 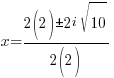 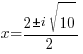 |
The solutions to the quadratic equation are 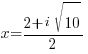 and
and 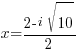 .
.
Example: Solve the quadratic equation by factoring.
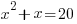
Solution:
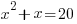 |
|
| Write the equation with all the terms on one side of the equation and zero on the other side of the equation. | 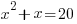 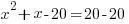 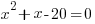 |
| Factor the expression on one side. | 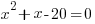 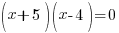 |
| Use the zero product property and set each factor equal to zero. | 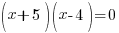 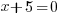 or or 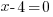 |
| Solve each equation. | 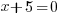 or or 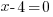 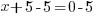 or or 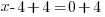 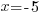 or or 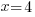 |
Check: 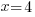
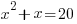
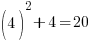
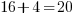
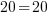
Since the value of 4 makes the equation true, 4 is a solution to the equation.
Check: 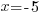
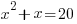
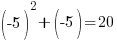
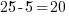
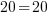
Since the value of -5 makes the equation true, -5 is a solution to the equation.
Example: Solve the quadratic equation by factoring.
 |
|
| The equation already has all of the terms on the same side and zero on the other side. |  |
| Factor the expression on one side. The expression for this equation is a difference of squares. |  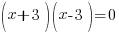 |
| Use the zero product property and set each factor equal to zero. | 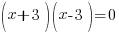 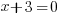 or or 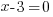 |
| Solve each equation. | 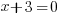 or or 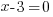 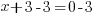 or or 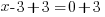 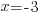 or or 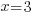 |
Example: Solve the quadratic equation with completing the square.

 |
|
| Rewrite the quadratic equation so that the square and everything that the square applies to are on one side of the equation. This is called isolating the square. |  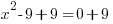 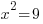 |
| Cancel out the square by square rooting both sides. | 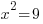 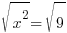 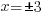 |
| The remaining equations are already solved. The solutions to the equation are 3 and -3. | 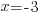 or or 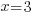 |
Example: Solve the quadratic equation by completing the square
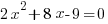
Solution:
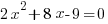 |
|
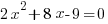 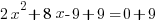 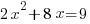 |
|
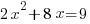 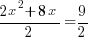 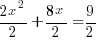 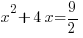 |
|
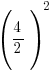 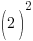 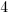 |
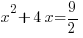 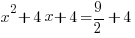 |
| The left hand side factors to be a perfect square | 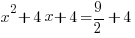 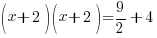 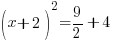 |
| Simplify the right hand side by finding a common denominator and adding the fractions. | 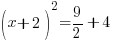 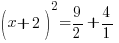 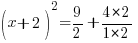 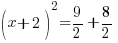 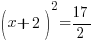 |
| Solve the equation using the square root method. Start by taking the square root of both sides to get rid of the square | 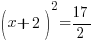 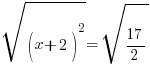 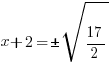 |
| Solve for x by subtracting 2 from both sides. | 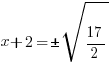 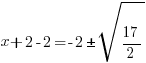 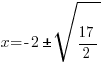 |
| Rationalize the denominator by applying the radical to the numerator and denominator | 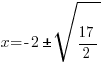 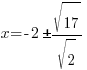 |
Rationalize the denominator by multiplying by the fraction 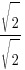 |
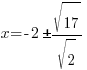 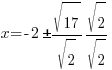 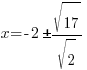 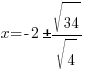 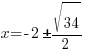 |
https://www.youtube.com/watch?v=tHxc3fO8yOo
Here is a youTube video with examples of using the square root method.