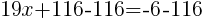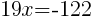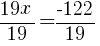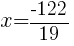Example: Solve the rational equation.
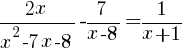
Solution:
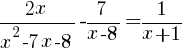
Since we are solving a rational equation we need to first find the restrictions (the values of x that cause the expression to be undefined).
To find the restrictions create an equation by setting each denominator equal to zero and solving.
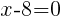
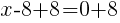
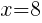
Having x=8 causes a zero in the denominator and the overall expression undefined. That makes 8 a restricted value .
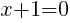
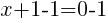
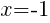
Having x=-1 causes a zero in the denominator and the overall expression undefined. That makes -1 a restricted value .
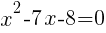
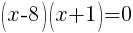
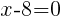 or
or 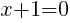
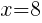 or
or 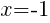
This gives the same restrictions we have already accounted for.
With the restriction in mind we will solve the equation.
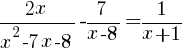 |
|
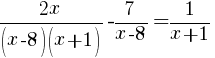 |
|
Multiply each side of the equation by the least common multiple of the denominators. For this equation the least common multiple is 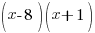 |
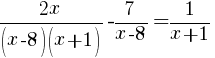 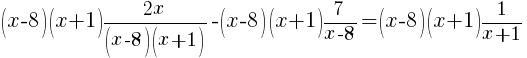 |
| Simplify by canceling the common factors. This should clear any denominators. | 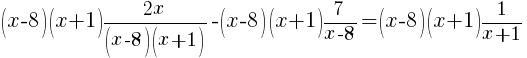 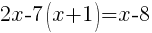 |
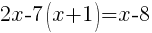 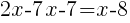 |
|
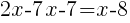 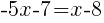 |
|
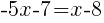 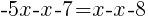 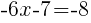 |
|
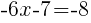 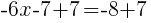 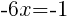 |
|
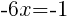 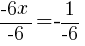 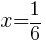 |
|
Video Example:
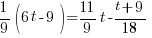
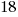 *
*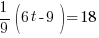 *
*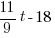 *
*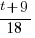
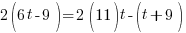
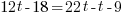
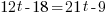
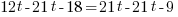
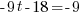
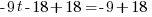
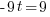
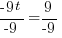
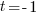
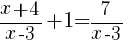
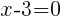
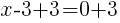
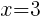
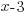
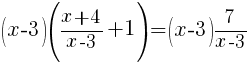
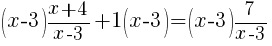
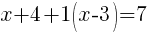
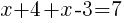
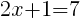
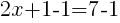
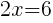
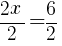
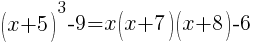
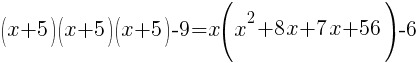
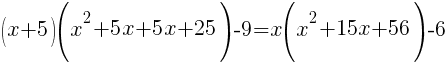
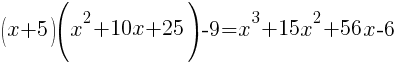
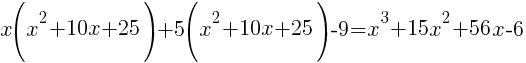
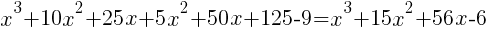
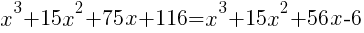
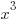 from each side. It cancels from each side.
from each side. It cancels from each side.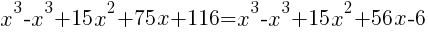
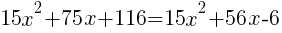
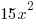 from each side. It cancels from each side.
from each side. It cancels from each side.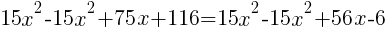
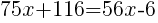
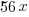 from each side and simplify.
from each side and simplify. 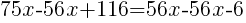
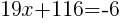
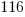 from each side and simplify.
from each side and simplify.